The Vecchia approximation and its descendants

Spatial Statistics - BIOSTAT 696/896

Michele Peruzzi

University of Michigan

Plan for the day

We will proceed the same way as for the Low Rank GP:

Define the joint distribution for any finite set of random variables
(Check Kolmogorov’s conditions)
Result: there is a stochastic process whose finite dimensional distribution is the one we chose

Vecchia’s approximation

Suppose X(s_1)=X_1, \dots, X(s_n)=X_n are random variables corresponding to realizations of a spatial process at locations s_1, \dots, s_n
Their joint density is \begin{align*} p(X_1, \dots, X_n) &= p(X_1) p(X_2 | X_1) p(X_3 | X_1, X_2) \cdots p(X_n | X_1, \dots, X_{n-1})\\ &= \prod_{i=1}^n p(X_i |\ \text{all}\ X_j\ \text{with}\ j<i) \end{align*}
Idea: we can approximate p(X_1, \dots, X_n) by dropping some variables from the conditioning sets, i.e. \begin{align*} p(X_1, \dots, X_n) &\approx \prod_{i=1}^n p(X_i |\ \text{some}\ X_j\ \text{with}\ j<i) \end{align*}

Vecchia’s approximation

\begin{align*} p(X_1, \dots, X_n) &\approx \prod_{i=1}^n p(X_i |\ \text{some}\ X_j\ \text{with}\ j<i) \end{align*} Define N_m(X_i) = \{ X_j : s_j \ \text{is one of the}\ m\ \text{nearest neighbors of}\ s_i\ \text{in the set}\ \{s_1, \dots, s_{i-1} \} \} Then, Vecchia’s approximation is

\begin{align*} p(X_1, \dots, X_n) &\approx \prod_{i=1}^n p(X_i | N_m(X_i)) \end{align*}

(Vecchia, 1988, JRSS-B)

DAG interpretation of Vecchia’s approximation

Draw a dense DAG
For every i \in \{1, \dots, n \} node, remove all i-1-m nodes that are not one of the m nearest neighbors
Result: a sparse DAG where each node is explained by at most m other nodes

Creating a stochastic process based on Vecchia’s approximation

Because we drop edges from a DAG, the resulting graphical model is also a DAG
Therefore, the collection of variables in the DAG have a joint density that factorizes according to the DAG
This means that there is a density p^* that factorizes according to the DAG, and \begin{align*} p(X_1, \dots, X_n) &\approx \prod_{i=1}^n p(X_i | N_m(X_i)) = p^*(X_1, \dots, X_n) \end{align*}
To create a stochastic process, we need to define the finite dimensional distributions for any finite set of random variables. Suppose our set is \{X_1, \dots, X_n\}, then we just take p^* as our joint density p^*(X_1, \dots, X_n) = \prod_{i=1}^n p(X_i | N_m(X_i))
Check Kolmogorov’s conditions
Assume all p(\cdot) are Gaussian
Obtain Nearesst-neighbor Gaussian Process (NNGP), Datta et al (2016)

Summary so far

For both LRGP and NNGP, we have used one method for creating a stochastic process

The method is

Draw a (sparse) DAG on n spatial nodes
Define a base density p to define relationships between nodes
Define a joint density p^* for those n nodes that factorizes according to the DAG
Assume the same joint density defines all finite dimensional distributions
(Check Kolmogorov’s conditions)
Obtain valid stochastic process based on p^*

Moving forward

The same method can be used to create other processes!
The key advantages of using DAGs are
- They lead to valid joint densities and valid stochastic processes
- They can be embedded easily within Bayesian hierarchical models
Remember that a DAG is aka Bayesian Network. All Bayesian models can be represented by a DAG

Covariance of a DAG-based spatial process model

We have seen that if X(\cdot) \sim GP, then Cov(X(s), X(s')) = C(s, s') where C(\cdot, \cdot) is the chosen covariance function
We have seen that this equivalence does not hold for a LRGP
It also does not hold for any other DAG-based model

Some literature on DAG-based methods

Meshed GPs (P et al, 2021) outlines a method for using DAGs on groups of locations and get a valid stochastic processes
By grouping locations, there is more freedom in choosing a specific DAG
Properties of the DAG can be used for even better computational performance
A multi-resolution approximation (MRA, Katzfuss 2017) has a DAG interpretation that extends to a stochastic process
A spatial multivariate tree (P & Dunson, 2022) also has a DAG interpretation
Bag of DAGs (Jin et al, 2023) uses an MGP setup but lets the DAG be unknown to allow for wind effects in non-stationary conditions
Radial neighbors GP (Zhu et al, 2023) defines a special DAG that facilitates theory development

Comparing LRGP and a DAG-based method

Simulate 2500 observations from a GP, a LRGP (225 knots), a NNGP (30 neighbors), and a QMGP (block size 100)
Use the same covariance function (exponential), with \sigma^2 = 1 and \phi = 2 for all models

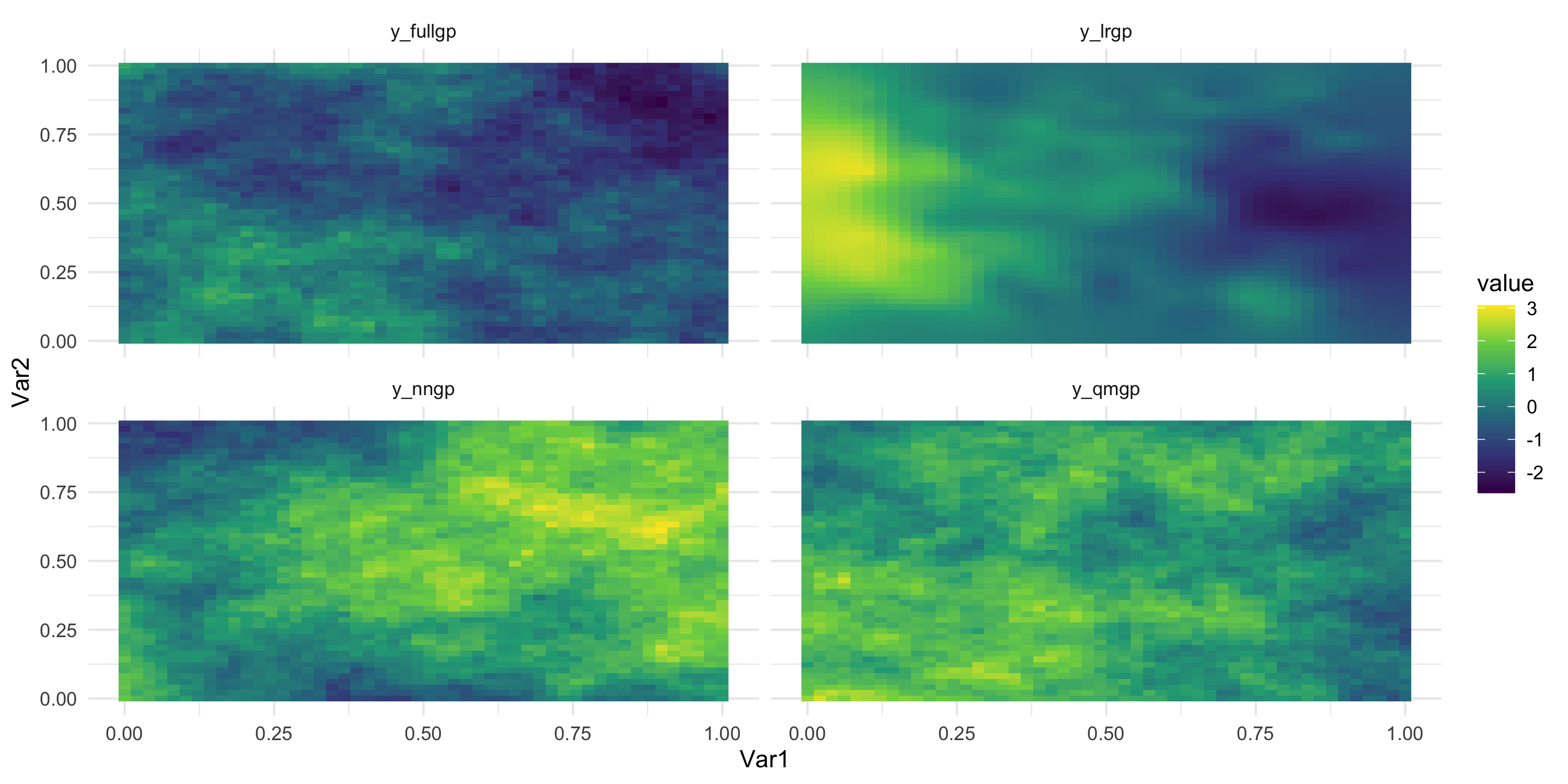
Comparing LRGP and a DAG-based method

\sigma^2 = 1 and \phi = 15 for all models

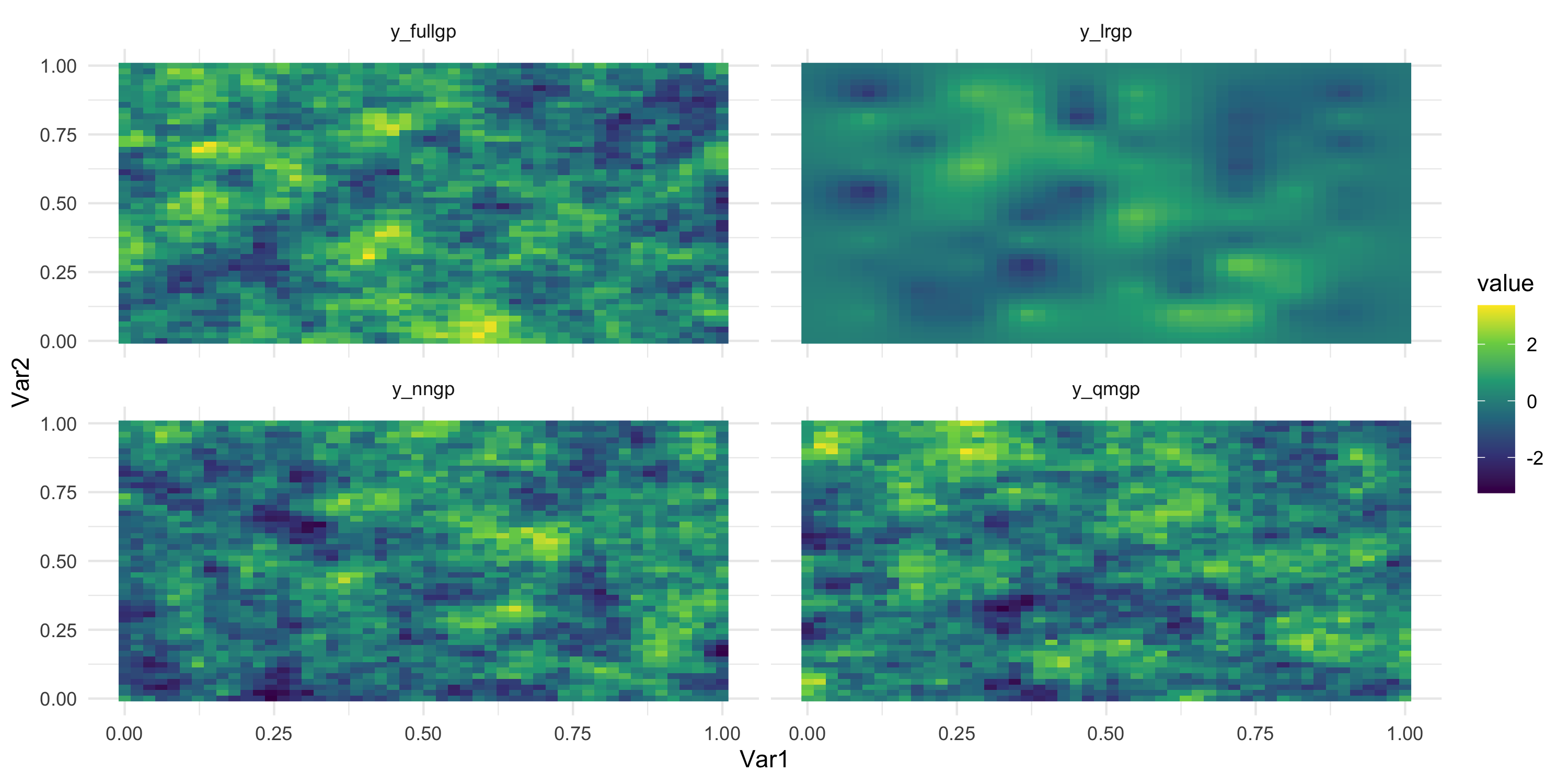
Homework?

Use R package spBayes to fit LRGP model to your dataset (use option knots=...)
Use R package spNNGP for the same purpose, following the package documentation
Use R package meshed for the same purpose, following the package documentation (bugs? let me know)

Response vs Latent models in DAG-based GPs

Remember Quiz 2?
Let’s revisit question 3

Response vs Latent models in DAG-based GPs

Model [1] is Y(\cdot) \sim \text{DAG-GP}(X(\cdot)^\top \beta, C_{\theta}(\cdot, \cdot), \text{other setup params}) where \beta is a vector of regression coefficients to which you associate a Gaussian prior \beta \sim N(0, V), and C_{\theta}(s, s') = \sigma^2 \exp\{ -\phi \| s-s' \| \} + \tau^2 1_{\{s=s'\}} is the exponential plus nugget covariance function. You assume \sigma^2 \sim Inv.G(a_s, b_s), \tau^2 \sim Inv.G(a_t, b_t), and \phi \sim U[3,30] as the prior distributions for the other unknowns in the model

Response vs Latent models in DAG-based GPs

Model [2] is Y = X\beta + w + \varepsilon where w(\cdot) \sim \text{DAG-GP}(0, C_{\theta}(\cdot, \cdot), \text{other setup params}) with C_{\theta}(s, s') = \sigma^2 \exp\{ -\phi \| s-s' \| \}, and \varepsilon \sim N(0, \tau^2 I_n). The other unknowns have priors \beta \sim N(0, V), \sigma^2 \sim Inv.G(a_s, b_s), \tau^2 \sim Inv.G(a_t, b_t), \phi \sim U[3,30].

Response vs Latent models in DAG-based GPs

The equivalence we have with GPs does not hold for DAG-based GPs
A DAG-based GP is constructed by taking a covariance function and then assuming conditional independence based on the DAG
Model 1 includes the nugget in the covariance, therefore the DAG also approximates the measurement error process. This is called a (DAG-based) response model
Model 2 excludes the nugget from the approximation. This is called a (DAG-based) latent model.
R package spNNGP allows you to fit NNGP models in their response and latent form
R package meshed fits a latent model based on a QMGP process

Gaussian linear systems and additional topics

Applying the usual properties of jointly Gaussian random variables:

\begin{align*} p(X_1, \dots, X_n) &= p(X_1) p(X_2 | X_1) \cdots p(X_n | X_1, \dots, X_n)\\ &= \prod_i^n p(X_i | X_{[1:i-1]}) = \prod_i^n N(X_i; H_i X_{[1:i-1]}, R_i) \end{align*}

can also be written as the linear system:

\begin{align*} X_1 &= \delta_1 \qquad \text{where} \qquad \delta_1 \sim N(0, R_1) \qquad \text{where}\qquad R_1 = \Sigma(1,1)\\ X_2 &= H_2 X_1 + \delta_2 \qquad\text{where} \qquad \delta_2 \sim N(0, R_2) \\ X_2 &= H_3 \begin{bmatrix} X_1 \\ X_2 \end{bmatrix} + \delta_3 \qquad\text{where} \qquad \delta_3 \sim N(0, R_3) \\ &\vdots\\ X_i &= H_i X_{[1:i-1]} + \delta_i \qquad\text{where} \qquad \delta_i \sim N(0, R_i) \\ &\vdots\\ X_n &= H_n X_{[1:n]} + \delta_n \qquad\text{where} \qquad \delta_n \sim N(0, R_n) \\ \end{align*}

From Gaussian densities to linear systems

The same linear system can be written as a single linear equation

\begin{align*} \begin{bmatrix} X_1 \\ X_2 \\ X_3 \\ \vdots \\ X_i \\ \vdots \\ X_n \end{bmatrix} &= \begin{bmatrix} 0 & \cdots \\ H_2 & 0 & \cdots \\ h_{3,1} & h_{3, 2} & 0 & \cdots \\ \cdots \\ h_{i, 1} & \cdots & h_{i, i-1} & 0 & \cdots \\ \cdots \\ h_{n, 1} & \cdots & \cdots & h_{n, n-1} & 0 \end{bmatrix}\begin{bmatrix} X_1 \\ X_2 \\ X_3 \\ \vdots \\ X_i \\ \vdots \\ X_n \end{bmatrix} + \begin{bmatrix} \delta_1 \\ \delta_2 \\ \delta_3 \\ \vdots \\ \delta_i \\ \vdots \\ \delta_n \end{bmatrix} \end{align*} in short \begin{align*} X &= \bm{H} X + \bm{\delta} \qquad \text{where} \qquad \bm{\delta} \sim N(0, D) \end{align*} where D is the diagonal matrix with ith diagonal element R_i.

From Gaussian densities to linear systems

This also implies: \begin{align*} (I_n - \bm{H}) X &= \bm{\delta} \\ (I_n - \bm{H})^{-1} (I_n - \bm{H}) X &= (I_n - \bm{H})^{-1} \bm{\delta}\\ X &= (I_n - \bm{H})^{-1} \bm{\delta} \end{align*} using properties of Gaussian vectors, X \sim N(0, (I_n - \bm{H})^{-1} D (I_n - \bm{H})^{-T}) which means that \begin{align*} \Sigma &= (I_n - \bm{H})^{-1} D (I_n - \bm{H})^{-T} \\ \Sigma^{-1} &= (I_n - \bm{H})^T D^{-1} (I_n - \bm{H}) \end{align*}

Linear systems of Gaussian random variables

Connection with Cholesky decomposition:

Suppose L is lower triangular such that L L^T = \Sigma
Notice that \bm{H} is also lower triangular, and so is (I_n - \bm{H})
However, (I_n - \bm{H})^{-1} is upper triangular
Therefore, \Sigma = (I_n - \bm{H})^{-1} D^{\frac{1}{2}} \cdot D^{\frac{1}{2}} (I_n - \bm{H})^{-T} is a different way to decompose \Sigma into the product of two triangular matrices
Similar property: det(\Sigma) = \prod_i d_{ii} where d_{ii} are the diagonal elements of D, hence d_{ii} = R_i

Linear systems of Gaussian random variables: DAG-based models

Applying the usual properties of jointly Gaussian random variables:

Call [i] the set of nodes in the DAG that have edges to i. This set is the conditioning set or set of parents of i.

\begin{align*} p^*(X_1, \dots, X_n) &= \prod_i^n p(X_i | X_{[i]}) = \prod_i^n N(X_i; H_i X_{[i]}, R_i) \end{align*}

This can also be written as the linear system:

\begin{align*} X_1 &= \delta_1 \qquad \text{where} \qquad \delta_1 \sim N(0, R_1) \qquad \text{where}\qquad R_1 = \Sigma(1,1)\\ X_2 &= H_2 X_{[2]} + \delta_2 \qquad\text{where} \qquad \delta_2 \sim N(0, R_2) \\ &\vdots\\ X_i &= H_i X_{[i]} + \delta_i \qquad\text{where} \qquad \delta_i \sim N(0, R_i) \\ &\vdots\\ X_n &= H_n X_{[n]} + \delta_n \qquad\text{where} \qquad \delta_n \sim N(0, R_n) \\ \end{align*}

The dimension of X_{[i]} depends on how many edges point to i in the DAG
In a nearest-neighbor model with m nearest neighbors, X_{[i]} is at most m \times 1 dimensional

From Gaussian densities to linear systems: DAG-based models

The same linear system can be written as a single linear equation

Unlike in a GP model, here h_{j, i} is 0 if j does not have an edge pointing to i
in short:

\begin{align*} X &= \bm{H} X + \bm{\delta} \qquad \text{where} \qquad \bm{\delta} \sim N(0, D) \end{align*}

where D is the diagonal matrix with ith diagonal element R_i
The matrix \bm{H} now has many zeros! It is a sparse (lower triangular) matrix

Using properties of Gaussian vectors, X \sim N(0, (I_n - \bm{H})^{-1} D (I_n - \bm{H})^{-T}) which means that

\begin{align*} \Sigma &= (I_n - \bm{H})^{-1} D (I_n - \bm{H})^{-T} \\ \Sigma^{-1} &= (I_n - \bm{H})^T D^{-1} (I_n - \bm{H}) \end{align*}

Now \bm{H} is sparse. It is nonzero at entry (j,i) if and only if j \to i in the DAG
What about \Sigma^{-1}?
We care about the sparsity of \Sigma^{-1} because it is related to the computational complexity of the model

Graphical model interpretation of multivariate Gaussian random variables

The moral graph is the undirected graphical model obtained from a DAG:
- if two nodes share a child but are not connected, connect them with an undirected edge (“moralization” or “marrying the parents”)
- replace all directed edges with undirected edges
In a Gaussian graphical model (like in our case):

Two nodes i and j are connected in the moral graph if and only if the (i,j) element of the precision matrix \Sigma^{-1} is nonzero

In other words, the pattern of zeros in the precision matrix (= inverse covariance) tells us about the connectedness of the underlying moral graph
Two nodes i and j are connected in the moral graph if:
- i \to j or j \to i
- i \to z and j \to z for some other node z (i.e., i and j are co-parents of z)

DAG-GPs are still GPs!

Suppose X(\cdot) \sim \text{DAG-GP}(0, C_{\theta}(\cdot, \cdot),\ \text{other model params})
“other model params” refers to, e.g., ordering of locations, number of neighbors, partitioning of the domain, size of the blocks – all of which are used to build the DAG
A consequence of any DAG-GP being a GP is that, for any finite set \{X_1, \dots, X_n\} and corresponding vector X: X \sim N(0, \tilde{C}_{\theta}) where \tilde{C}_{\theta}^{-1}=(I_n - \bm{H})^T D^{-1} (I_n - \bm{H}) with \bm{H} and D defined as previously, based on the sparse DAG.
Because for any finite set of random variables, the finite dimensional distribution is Gaussian, the resulting process is a GP
The resulting DAG-GP has a covariance function that is not C_{\theta}(\cdot, \cdot)
Because C_{\theta}(\cdot, \cdot) is used to define the DAG-GP, it is called the base covariance function

Posterior sampling for DAG-based methods

We have seen two main different types of models using DAG-GPs.

Response model
Latent model

Each strategy leads to separate MCMC alternatives. We will consider 3 MCMC alternatives for each model.

Response model, option 1

Y(\cdot) \sim \text{DAG-GP}(X\beta, C_{\theta}(\cdot, \cdot), \ \text{other model params})

C_{\theta}(\cdot, \cdot) is any valid covariance function
Nugget included in the covariance function
MCMC uses the following density as target Y|\beta, \theta \sim N(X\beta, \tilde{C}_{\theta})
This density is very simple to compute because \tilde{C}_{\theta}^{-1}=(I_n - \bm{H})^T D^{-1} (I_n - \bm{H}) and det(\tilde{C}_{\theta}) = \prod_i d_{ii}
MCMC then targets \beta, \theta jointly

Response model, option 2: not as good

Suppose we marginalize \beta, then Y|\theta \sim N(0, X V_{\beta} X^T + \tilde{C}_{\theta})
However in this latter case we must compute (X V_{\beta} X^T + \tilde{C}_{\theta})^{-1}, but this is expensive
Woodbury matrix identity? (X V_{\beta} X^T + \tilde{C}_{\theta})^{-1} = \tilde{C}_{\theta}^{-1} - \tilde{C}_{\theta}^{-1} X (V_{\beta}^{-1} + X^T \tilde{C}_{\theta}^{-1} X)^{-1} X^T \tilde{C}_{\theta}^{-1} may help

Response model, option 3

Y(\cdot) \sim \text{DAG-GP}(X\beta, C_{\theta}(\cdot, \cdot), \ \text{other model params}) - C_{\theta}(\cdot, \cdot) is any valid covariance function - Nugget included in the covariance function - MCMC uses a Metropolis-within-Gibbs scheme:

Update \theta | \beta, Y via Metropolis, targeting p(\theta | Y, \beta) \propto p(Y | \beta, \theta) p(\theta). Like before, Y|\beta, \theta \sim N(X\beta, \tilde{C}_{\theta})
Update \beta | \theta, Y via a Gibbs step. In fact we can write Y = X\beta + \eta where \eta \sim N(0, \tilde{C}_{\theta}). Because \theta is considered known, we have

\begin{align*} \beta | \theta, Y &\sim N(\mu^*, V^*)\\ V^{-1^*} &= V_{\beta}^{-1} + X^T \tilde{C}_{\theta}^{-1} X\\ \mu^* &= V^*X^T \tilde{C}_{\theta}^{-1} Y \end{align*}

Comment on the complexity of sampling \beta.

Latent model

In this case, we write the Bayesian hierarchical model as

\begin{align*} \theta &\sim p(\theta) \\ \tau^2 &\sim InvG(a_{\tau}, b_{\tau})\\ \beta | \tau^2 &\sim N(0, \tau^2 V_{\beta})\\ w(\cdot) | \theta &\sim \text{DAG-GP}(0, C_{\theta}(\cdot, \cdot), \text{other model params)} \\ Y | \beta, w, \theta &\sim N(X\beta + w, \tau^2 I_n) \end{align*}

MCMC sampling everything is Metropolis-within-Gibbs:

Update \theta using Metropolis step
Sample \tau^2 | w, \beta, Y via Gibbs step. Any guess what this distribution is?
Sample \beta | \tau^2, w, Y via Gibbs step. Any guess what this distribution is?
Sample w | \beta, \tau^2, Y via Gibbs step. Any guess what this distribution is?

Latent model, option 1 – block sampler

Sample w | \beta, \tau^2, Y via Gibbs step as a block, i.e. update the whole vector w at once
Write the model in the usual linear regression form:

\tilde{Y} = I_n w + \varepsilon,\ \text{where} \ \varepsilon \sim N(0,\tau^2 I_n)

All parameters are known except for w and the prior is w \sim N(0, \tilde{C}_{\theta})
Therefore the full conditional posterior is:

\begin{align*} w | Y, \tau^2, \beta, \theta &\sim N( \mu_w, \Sigma_w )\\ \Sigma_w^{-1} &= \tilde{C}_{\theta}^{-1} + 1/\tau^2 \\ \mu_w &= \Sigma_w (Y - X\beta)/\tau^2 \end{align*}

We do not need to compute \Sigma_w to sample w
We can sample w using a conjugate gradient algorithm (see Nishimura and Suchard 2022)
Zhu et al 2024 uses this method for the RadGP model, R package at https://github.com/mkln/RadGP

Latent model, option 2 – DAG sampler

Remember our prior is w(\cdot) \sim \text{DAG-GP}
This implies we can write the DAG for w as a hierarchy
Refer to w_i as the random variable/vector associated to node i in the DAG
Refer to w_{[i]} as the random vector of parents of i in the DAG, i.e. [i] = \{ j: j\to i \}
Then we have (everything below is conditioned on \theta)

\begin{align*} w_1 | w_{[1]}, \theta &\sim N(H_1 w_{[1]}, R_1) \\ w_2 | w_{[2]}, \theta &\sim N(H_2 w_{[2]}, R_2) \\ \vdots & \\ w_i | w_{[i]}, \theta &\sim N(H_i, w_{[i]}, R_i) \\ \vdots & \\ w_M | w_{[M]}, \theta &\sim N(H_M, w_{[M]}, R_M) \end{align*}

Here M is the last node in the DAG. If 1 node = 1 random variable, then M = n

Latent model, option 2 – DAG sampler

The Bayesian hierarchical model is

Latent model, option 2 – DAG sampler

The Bayesian hierarchical model is

\begin{align*} \theta &\sim p(\theta) \\ \tau^2 &\sim InvG(a_{\tau}, b_{\tau})\\ \beta | \tau^2 &\sim N(0, \tau^2 V_{\beta})\\ w_1 | w_{[1]}, \theta &\sim N(H_1 w_{[1]}, R_1) \\ \vdots & \\ w_i | w_{[i]}, \theta &\sim N(H_i, w_{[i]}, R_i) \qquad \qquad \qquad w = \begin{bmatrix} w_1^\top & \cdots & w_M^\top \end{bmatrix}^\top \\ \\ \vdots & \\ w_M | w_{[M]}, \theta &\sim N(H_M, w_{[M]}, R_M) \\ Y | \beta, w, \theta &\sim N(X\beta + w, \tau^2 I_n) \end{align*}

We then consider this extended DAG for posterior sampling
Updating \theta, \beta, \tau^2 proceeds exactly as before
We then need to update w_i | w_{-i}, Y, \beta, \tau^2, where w_{-i} corresponds to all nodes except i

Latent model, option 2 – DAG sampler

What is w_i | w_{-i}, Y, \beta, \tau^2?
This is a Gaussian density that depends on:
- Parents in the DAG: w_{[i]}
- Children in the DAG: w_{j} such that i \in [j]
- Co-parents in the DAG: w_{j} such that j \to z and i \to z for some z in the DAG
We can sample together as a block all i that have the same color in the DAG
Color of a node is associated to the concept of clique in the DAG
A DAG with fewer colors has larger blocks and leads to faster, more efficient sampling
Refer to P et al 2021 JASA and P and Dunson 2022
R packages meshed and spNNGP (using “latent” option) use this method

Latent model, option 3 – marginal or collapsed sampler

The Bayesian hierarchical model is

\begin{align*} \theta &\sim p(\theta) \\ \tau^2 &\sim InvG(a_{\tau}, b_{\tau})\\ \beta | \tau^2 &\sim N(0, \tau^2 V_{\beta})\\ w | \theta &\sim N(0, \tilde{C}_{\theta}) \\ Y | \beta, w, \theta &\sim N(X\beta + w, \tau^2 I_n) \end{align*}

Then, marginally we have

\begin{align*} \theta &\sim p(\theta) \\ \tau^2 &\sim InvG(a_{\tau}, b_{\tau})\\ \beta | \tau^2 &\sim N(0, \tau^2 V_{\beta})\\ Y | \beta, \theta &\sim N(X\beta + w, \tilde{C}_{\theta} + \tau^2 I_n) \end{align*}

What is the problem with \tilde{C}_{\theta} + \tau^2 I_n?

Latent model, option 3 – marginal or collapsed sampler

In all DAG-GP models:

We can easily build \tilde{C}_{\theta}^{-1} and related quantities
We never want to work with \tilde{C}_{\theta} because that is dense
Careful about how we are treating \tilde{C}_{\theta}^{-1}
The collapsed sampler is a good example of potential problems

We use the Woodbury matrix identity:

\begin{align*} (\tilde{C}_{\theta} + \tau^2 I_n)^{-1} &= \frac{1}{\tau^2} I_n - \left( \frac{1}{\tau^4} \right)^2 \left( \tilde{C}_{\theta}^{-1}/\tau^2 + I_n \right)^{-1} \end{align*}

This identity allows us to work with \tilde{C}_{\theta}^{-1} rather than \tilde{C}_{\theta}
Notice we need to compute \left( \tilde{C}_{\theta}^{-1}/\tau^2 + I_n \right)^{-1}
This is the inverse of a sparse symmetric positive definite matrix
No easy way to do it: need to do Cholesky
Cholesky decompositions for sparse symmetric-pd matrices are faster than the dense case, but not very fast in general