Point-referenced spatial data

Spatial Statistics - BIOSTAT 696/896

Michele Peruzzi

University of Michigan

Recap: point-referenced spatial data

  • We observe Y(s) at location s
  • What is s in this case?
  • What are some examples of point-referenced data?

Point-referenced spatial data

  • Observe Y(s) at s \in \cal L = \{s_1, \dots, s_n\}
  • The set \cal L is assumed fixed and known, ie the locations are not random

Goals

  • Learn/estimate how Y(\cdot) changes in space. Model the spatial dependence
  • Generalize linear regression: drop i.i.d. assumption in favor of spatial dependence
  • Predict Y(\cdot) at locations that were not observed

Example

  • How does air pollution spread geographically?
  • Considering the impact of air pollution on health, how should we model the spread of respiratory disease?
  • Using a fixed set of observations of air pollution, how can we estimate the level of air pollution everywhere else?

Exploratory analysis and simulation

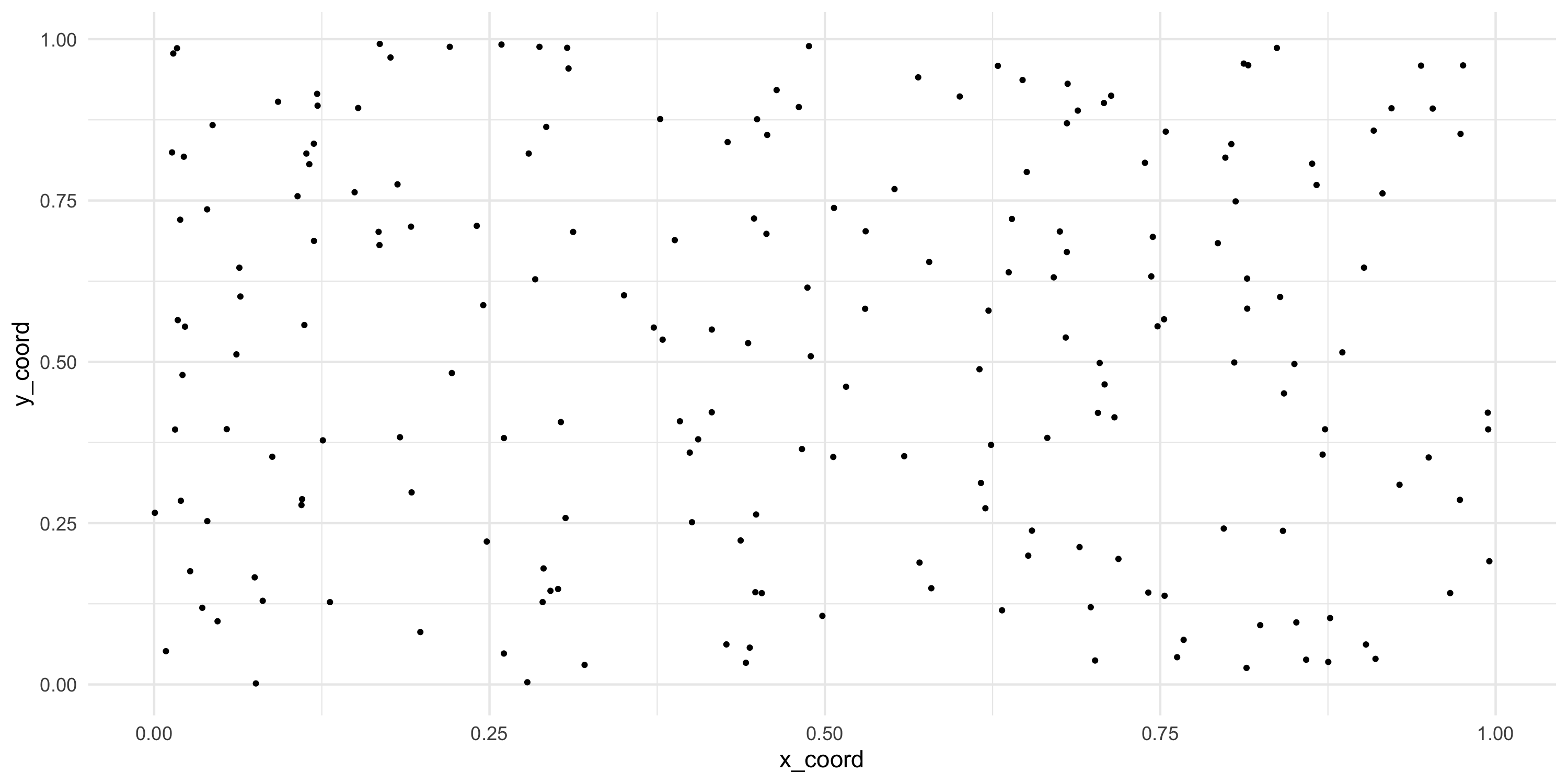
  • Simulating a fixed set of spatial locations
  • This is just for simulation. Remember with point-referenced data the coordinates are given and non-random
  • Remember to set the seed for reproducible analyses!!
set.seed(2024) # set a seed

n_obs <- 200
x_coord <- runif(n_obs, 0, 1)
y_coord <- runif(n_obs, 0, 1)
coords <- data.frame(x_coord, y_coord)

Plotting

library(tidyverse)

ggplot(coords, aes(x_coord, y_coord)) +
  geom_point(size=.7) +
  theme_minimal()

Exploratory analysis and simulation

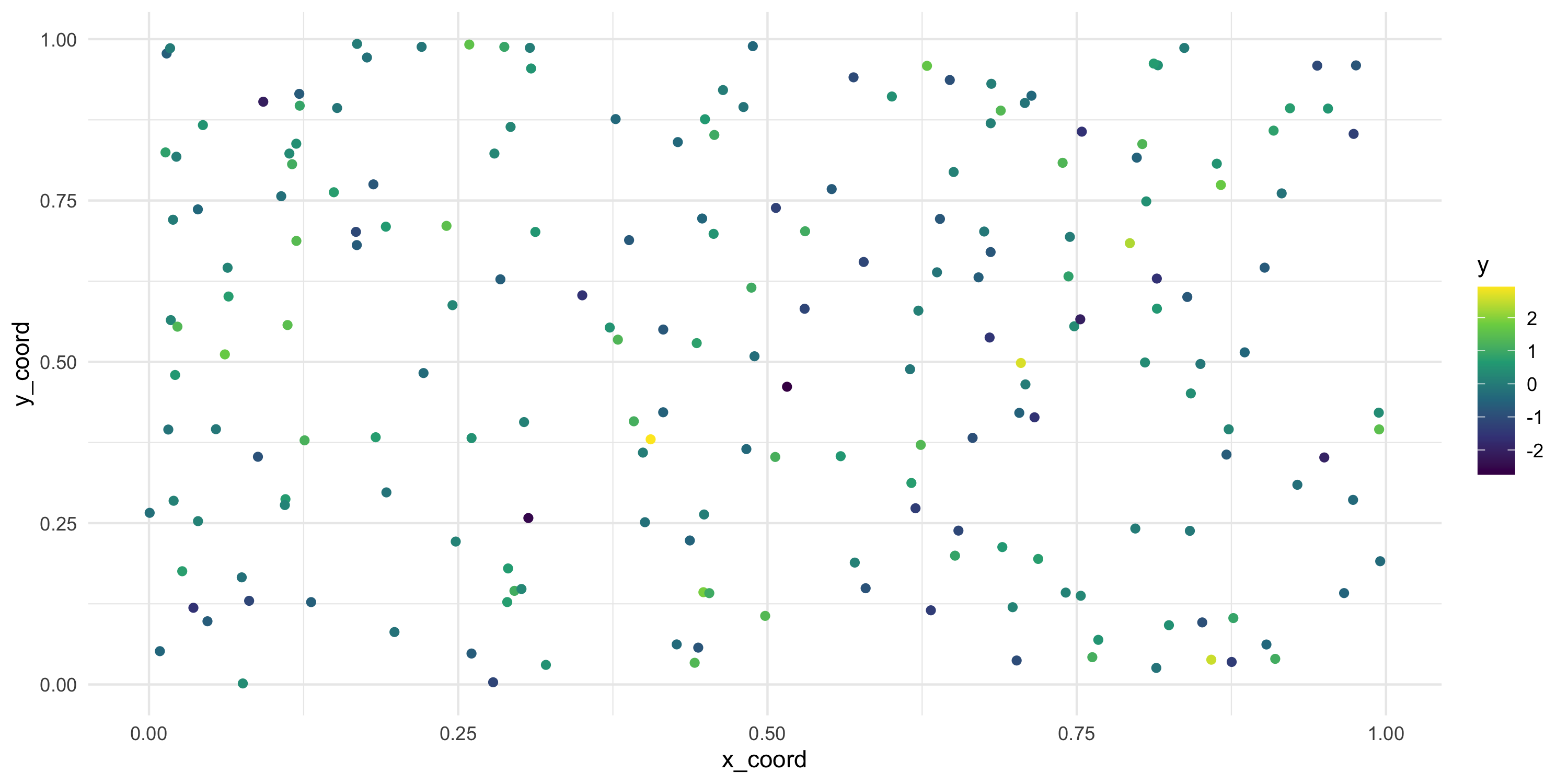
  • We just have locations now, there is no data. Let’s generate some data for those locations
  • No need to set the seed here. The script will run from the beginning and do all RNGs in sequence
  • You can set the seed here if you expect to run chunks of code in different sequences
#set.seed(1234) 
y <- rnorm(n_obs, 0, 1)
  • How many random variables are we generating?
  • What do you expect to see when we plot y on the coordinates we had before? Why?

Exploratory analysis and simulation

df <- coords %>% mutate(y=y)

ggplot(df, aes(x_coord, y_coord, color=y)) +
  geom_point() +
  theme_minimal() +
  scale_color_viridis_c()

Exploratory analysis and simulation

Make it easier to see there is no spatial dependence by

  • increasing sample size
n_obs <- 20000
x_coord <- runif(n_obs, 0, 1)
y_coord <- runif(n_obs, 0, 1)
coords <- data.frame(x_coord, y_coord)
y <- rnorm(n_obs, 0, 1)
df <- coords %>% mutate(y=y)

ggplot(df, aes(x_coord, y_coord, color=y)) +
  geom_point(size=.5) +
  theme_minimal() +
  scale_color_viridis_c()

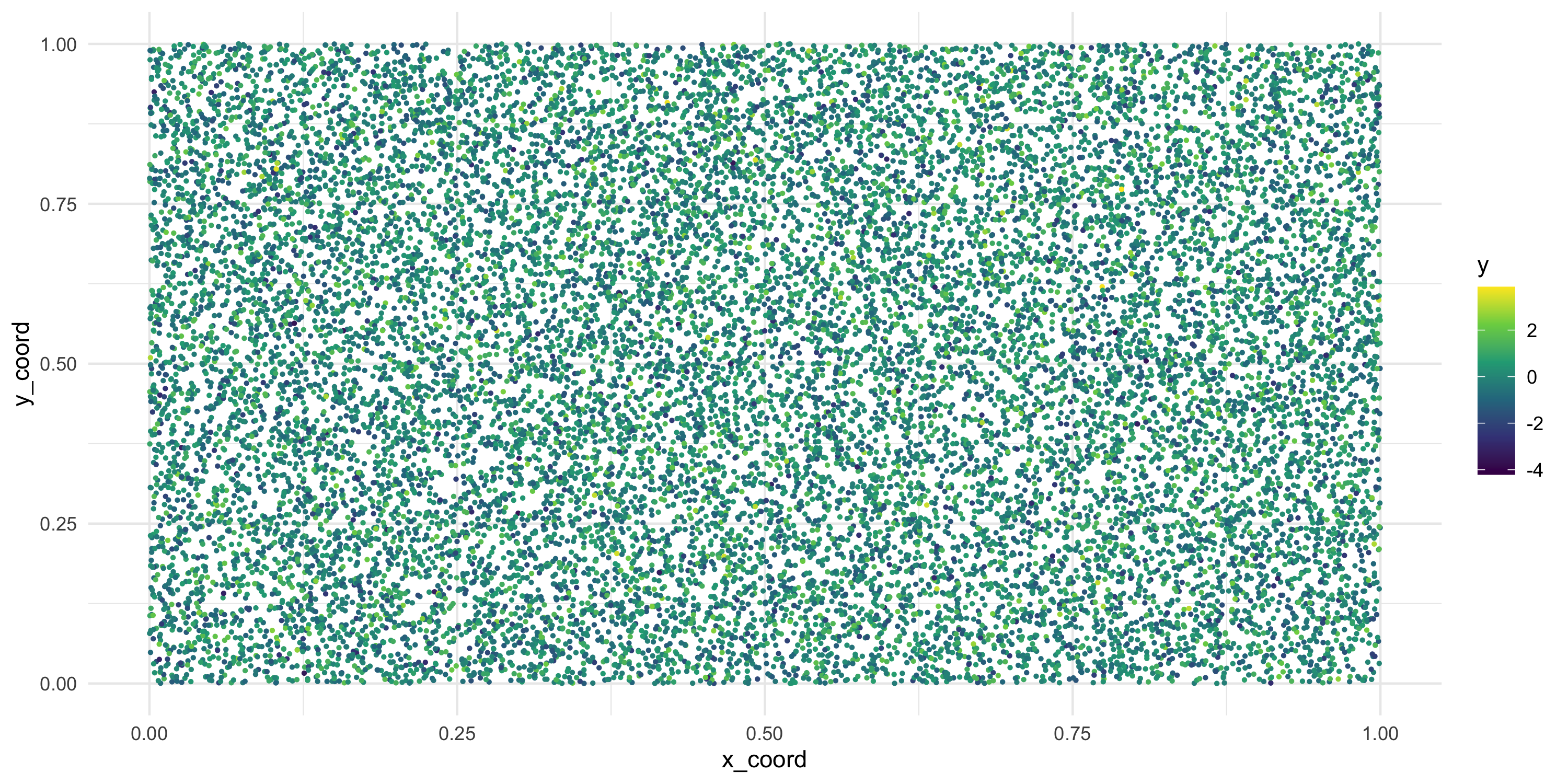
Exploratory analysis and simulation

Make it easier to see there is no spatial dependence by

  • plotting on a regular grid of spatial locations
  • regular grid = each data point can be plotted as a pixel on a raster image
coords <- expand.grid(xlocs <- seq(0,1,length.out=100), xlocs) 
n_obs <- nrow(coords)
y <- rnorm(n_obs, 0, 1)
df <- coords %>% mutate(y=y)

ggplot(df, aes(Var1, Var2, fill=y)) +
  geom_raster() +
  theme_minimal() +
  scale_fill_scico(palette="batlowK")

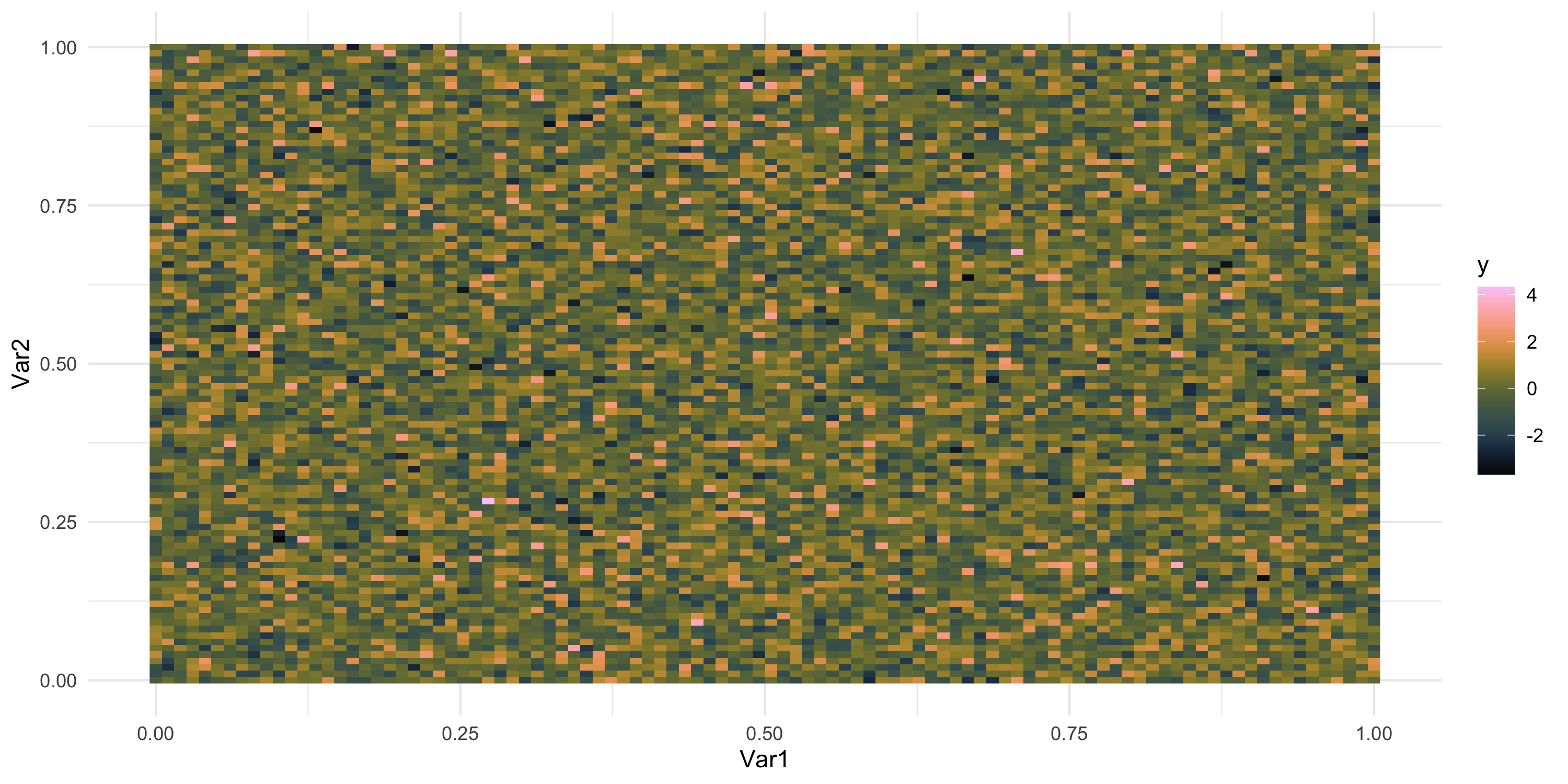
Exploratory analysis and simulation

  • We have seen simulated spatial data without spatial dependence
  • What would we expect to see if there was spatial dependence?
  • Can you think of ways we could simulate data with spatial dependence?

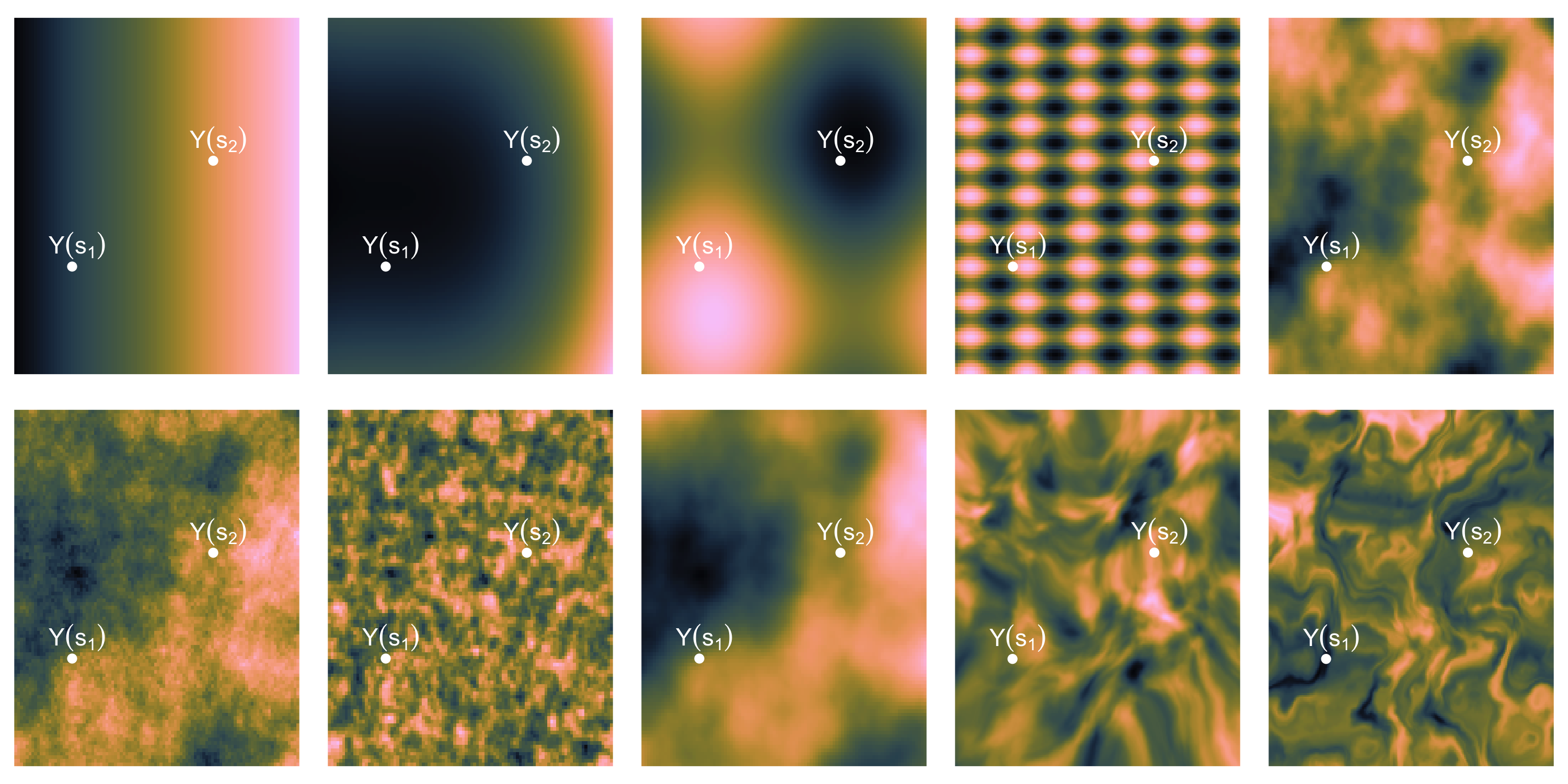
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 1

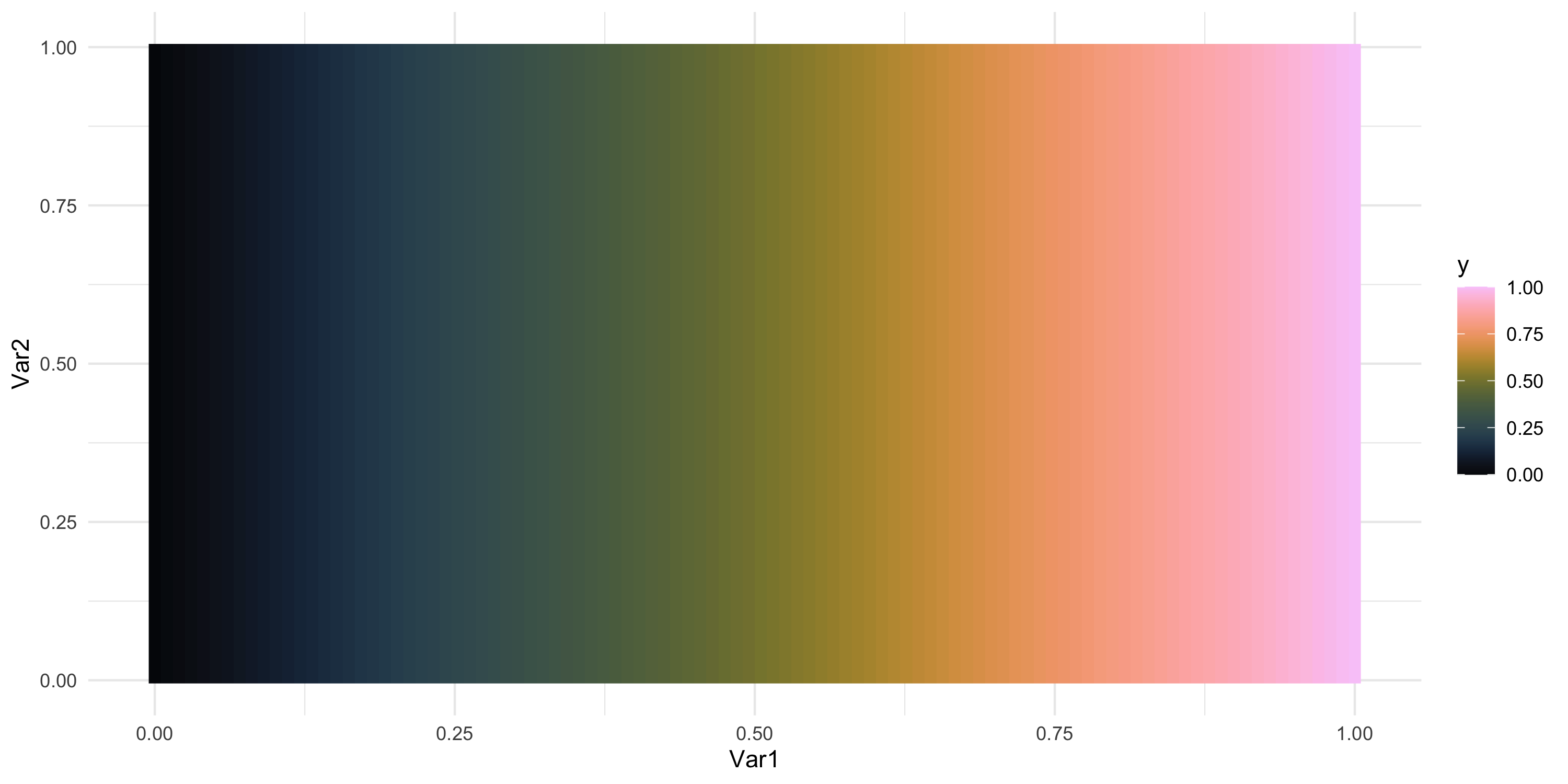
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 2

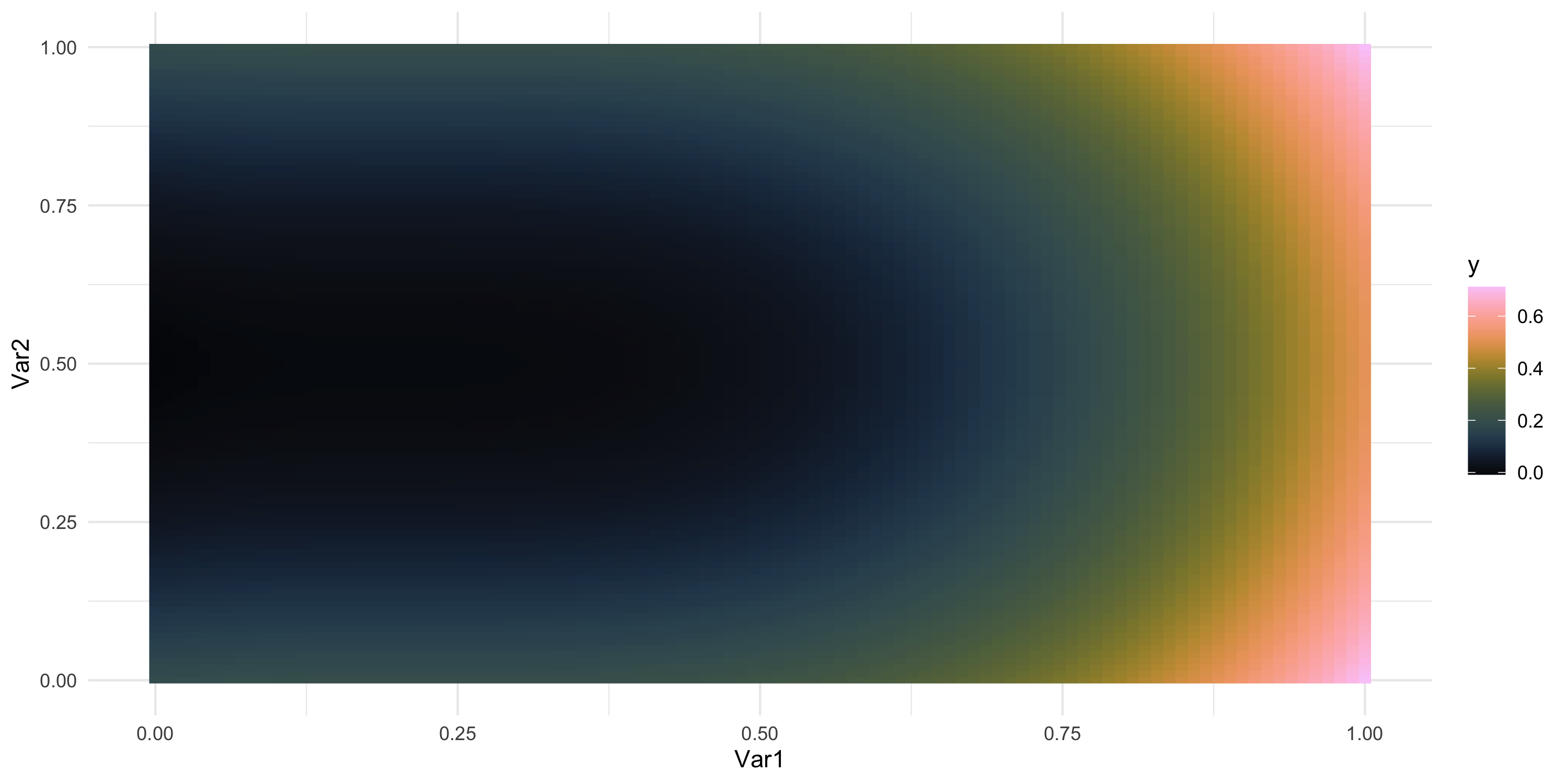
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 3

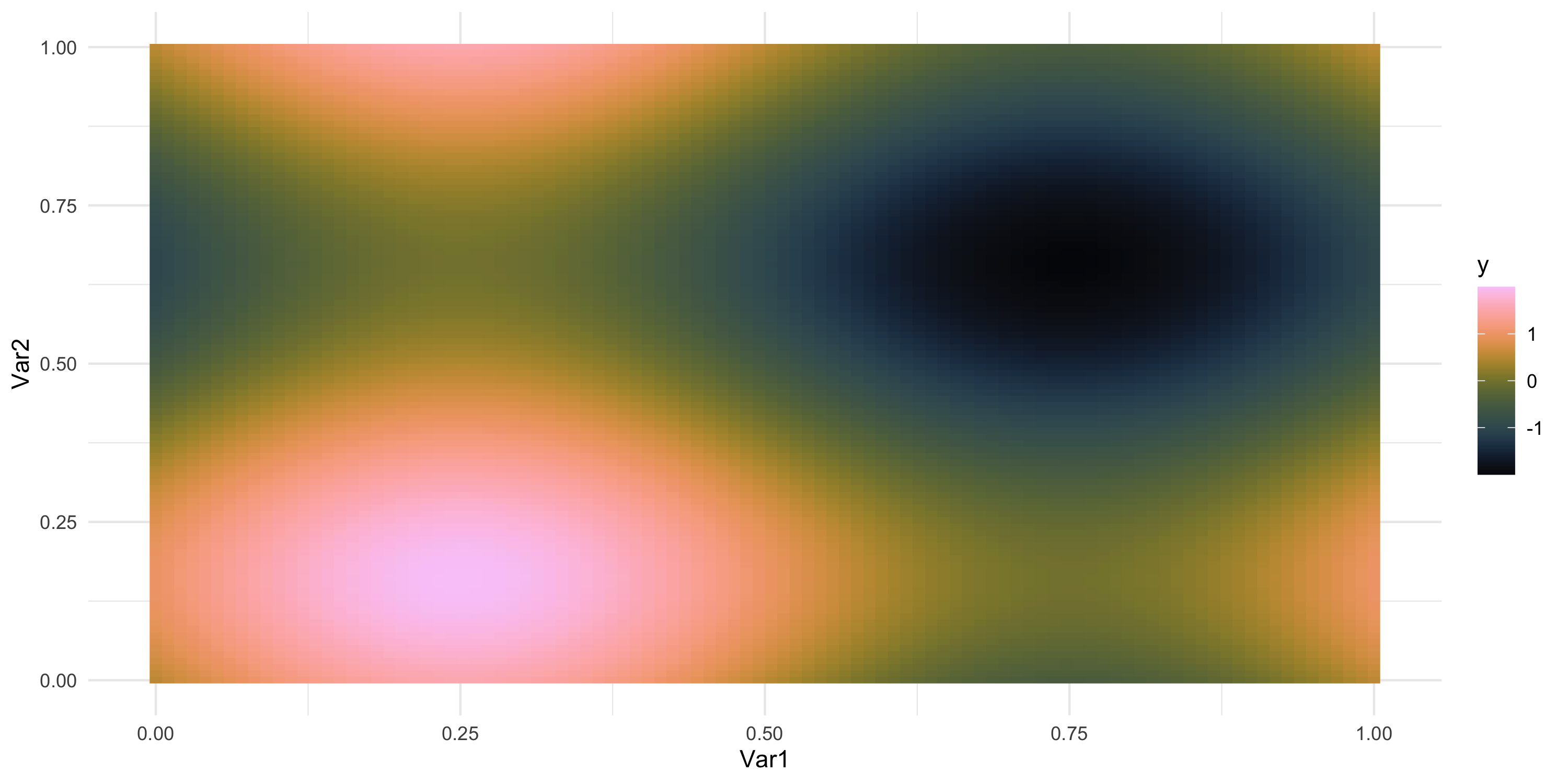
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 4

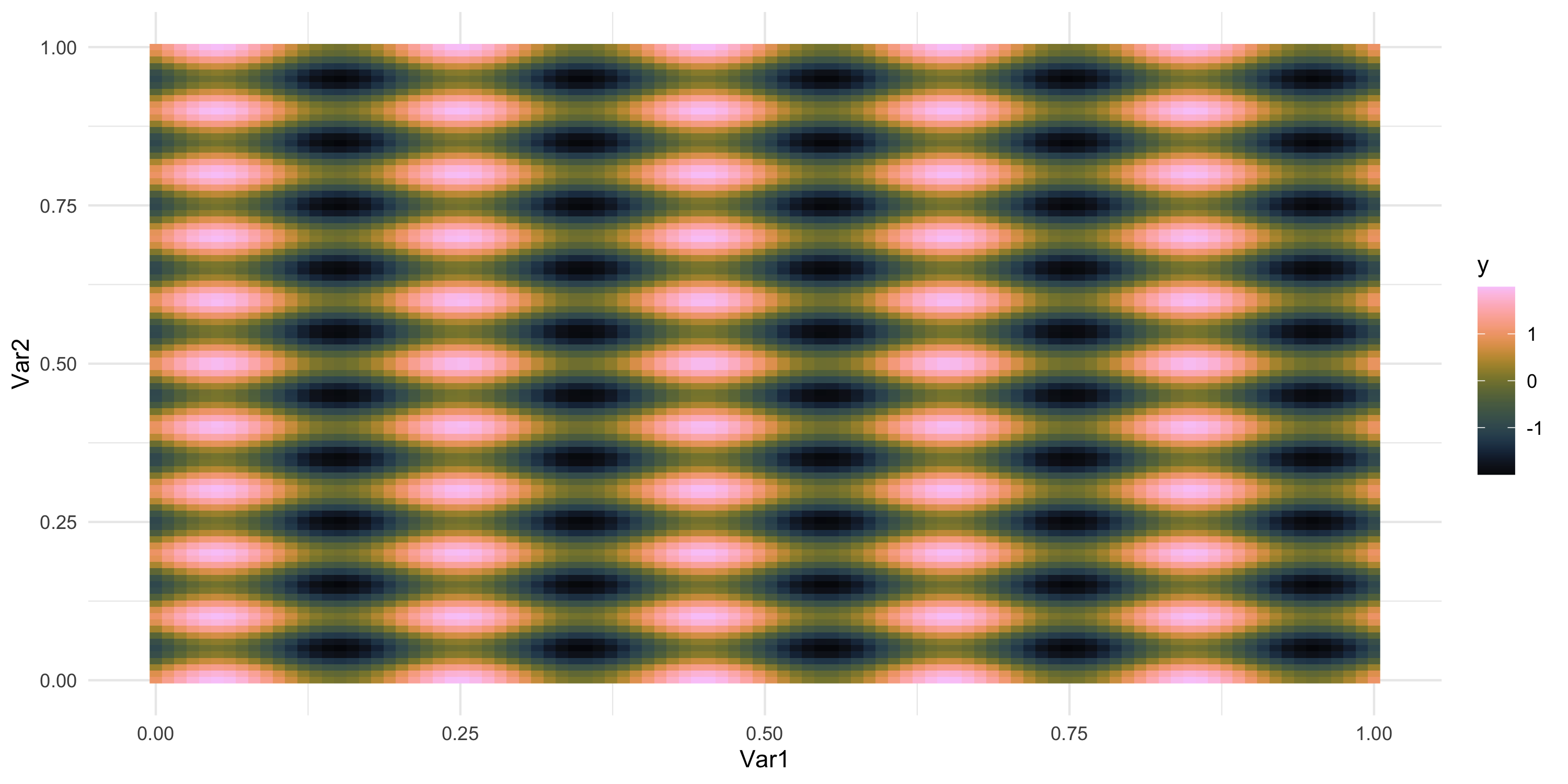
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 5

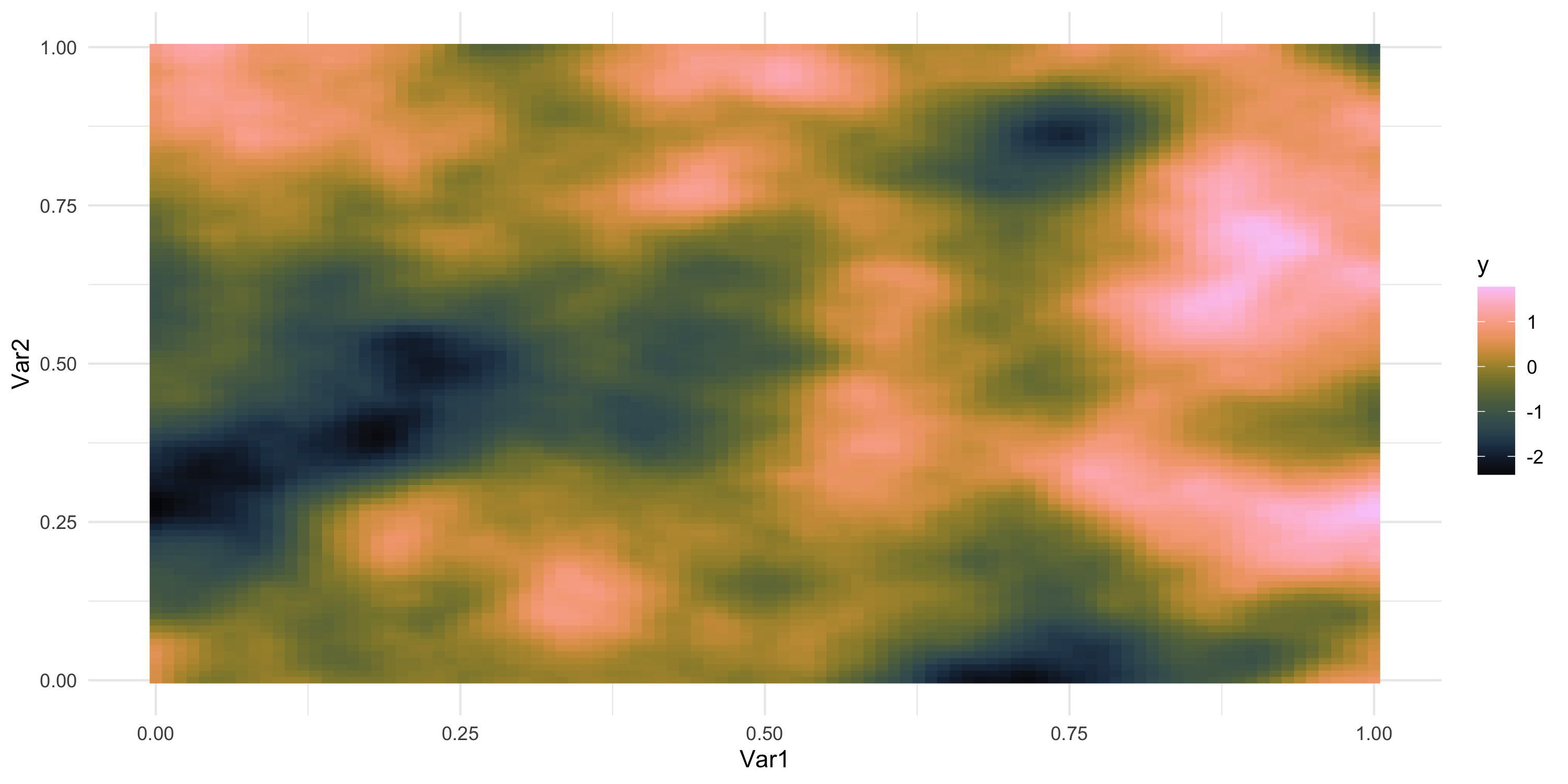
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 6

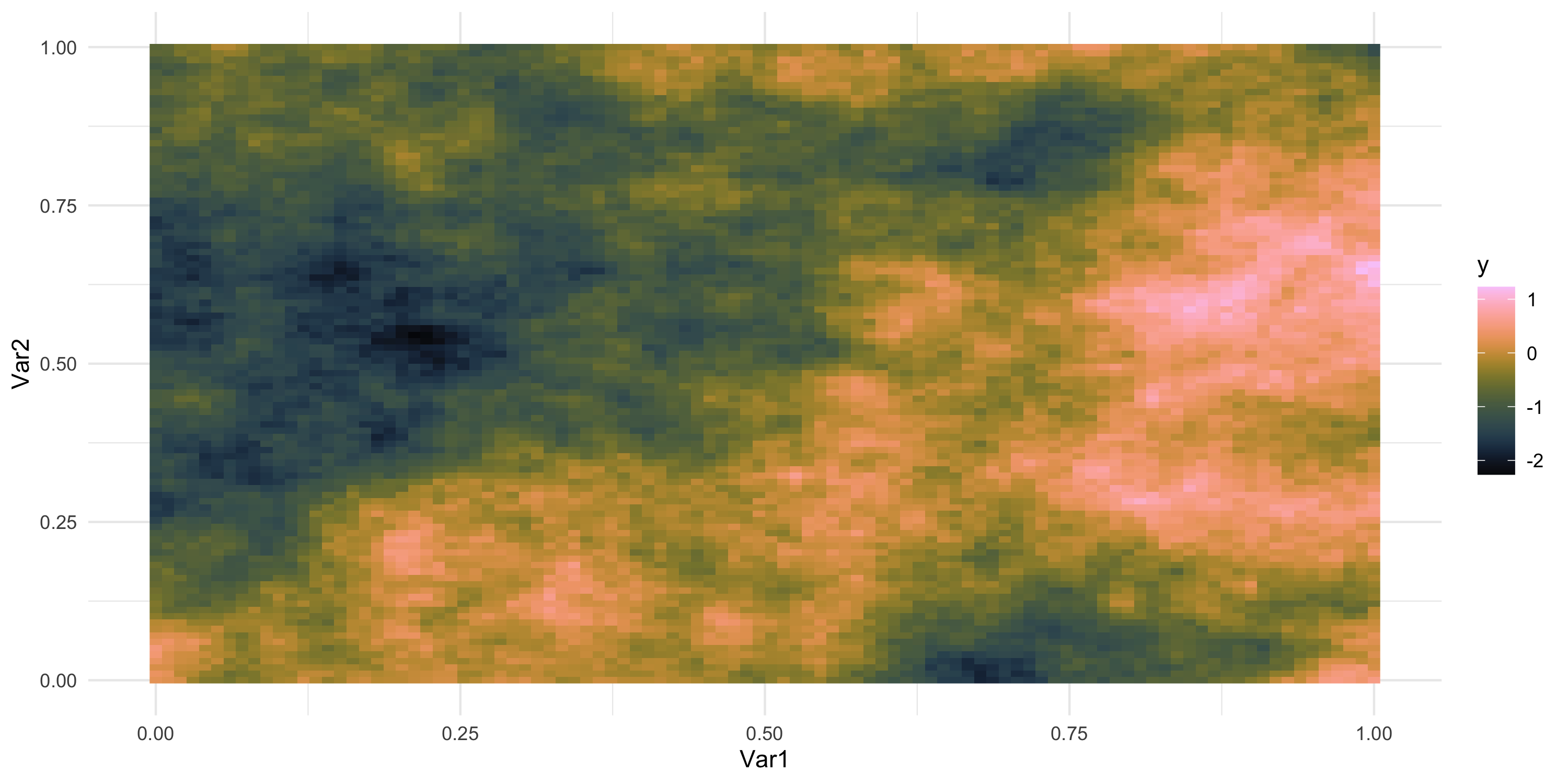
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 7

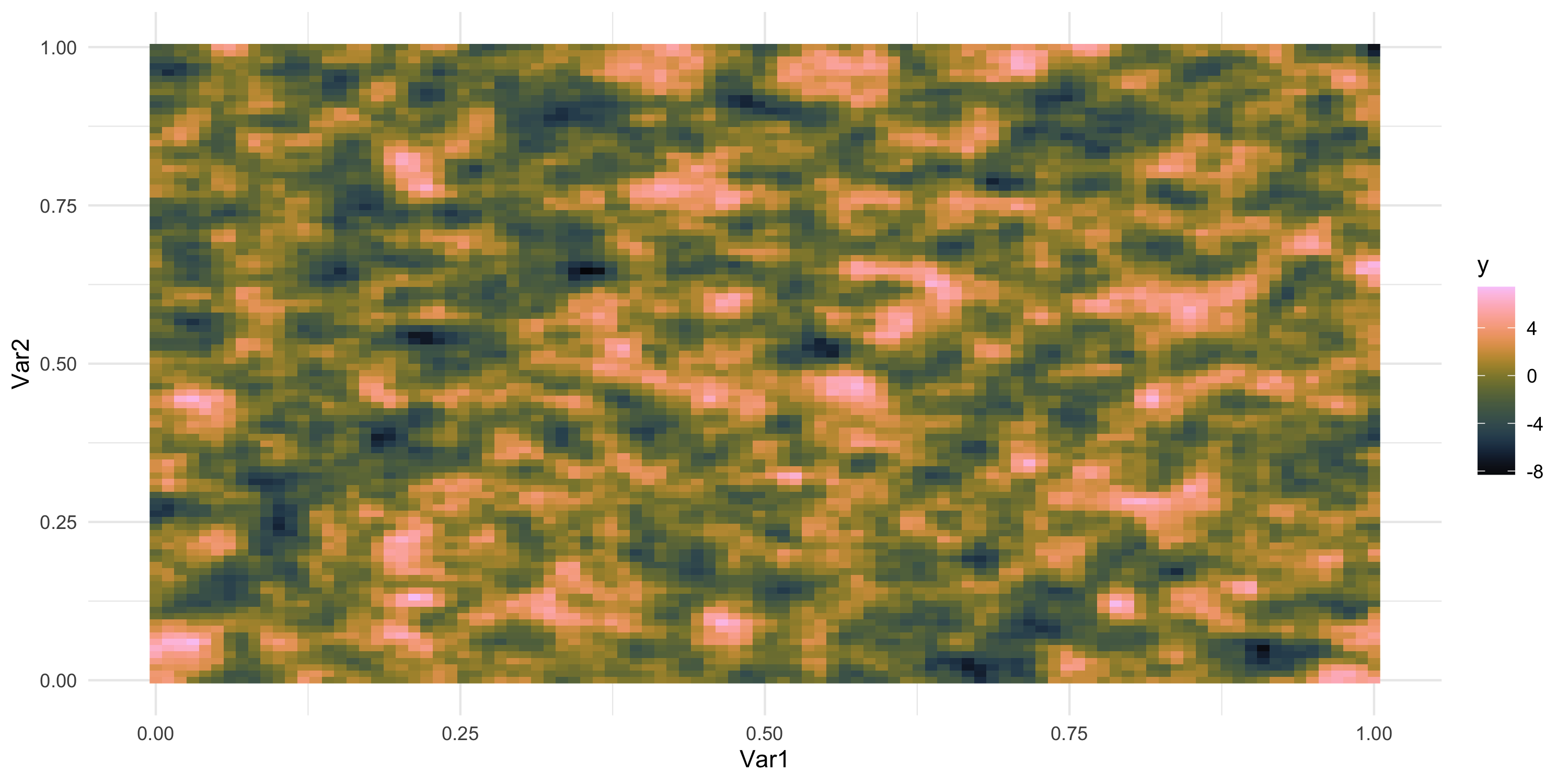
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 8

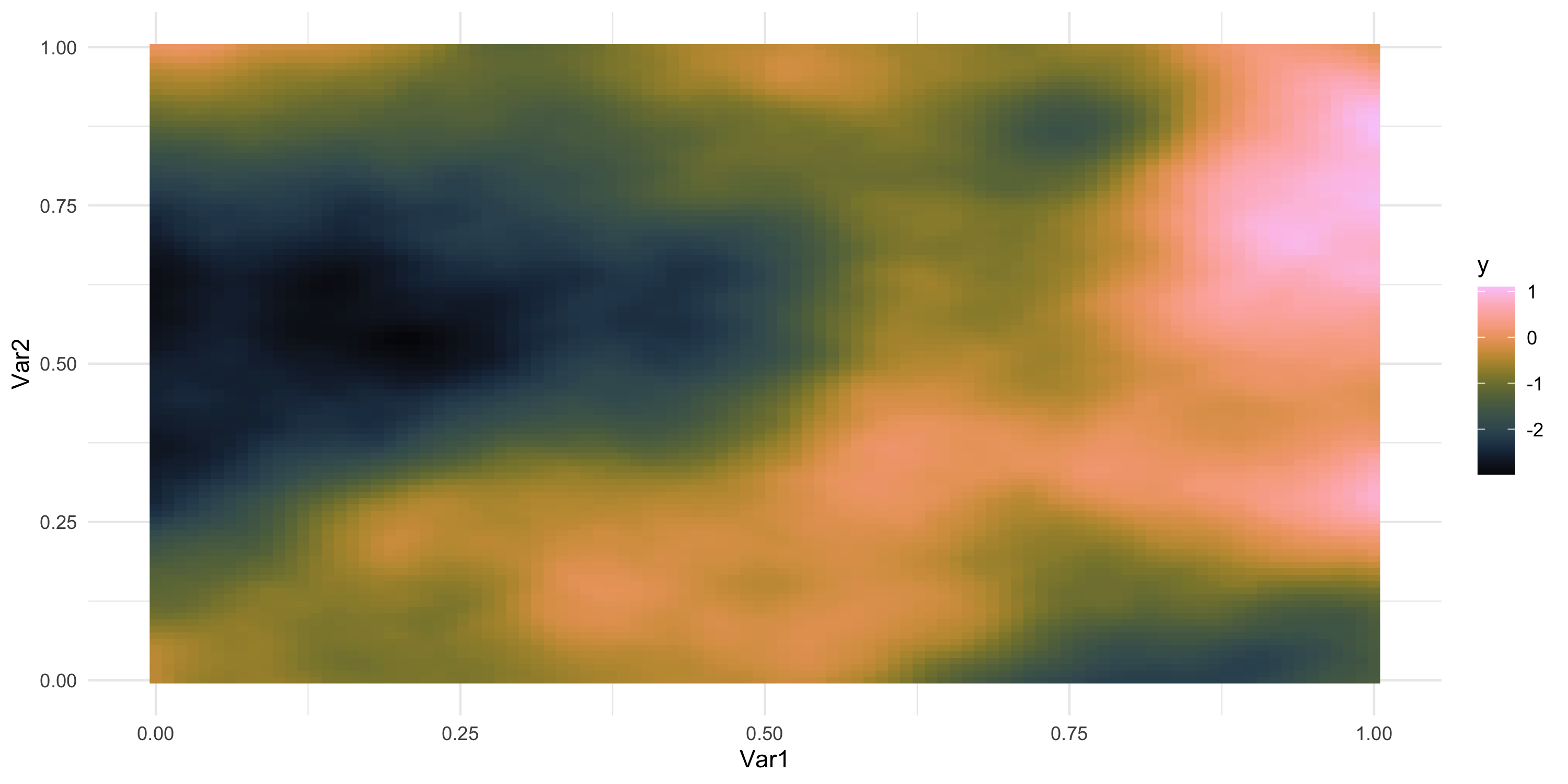
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 9

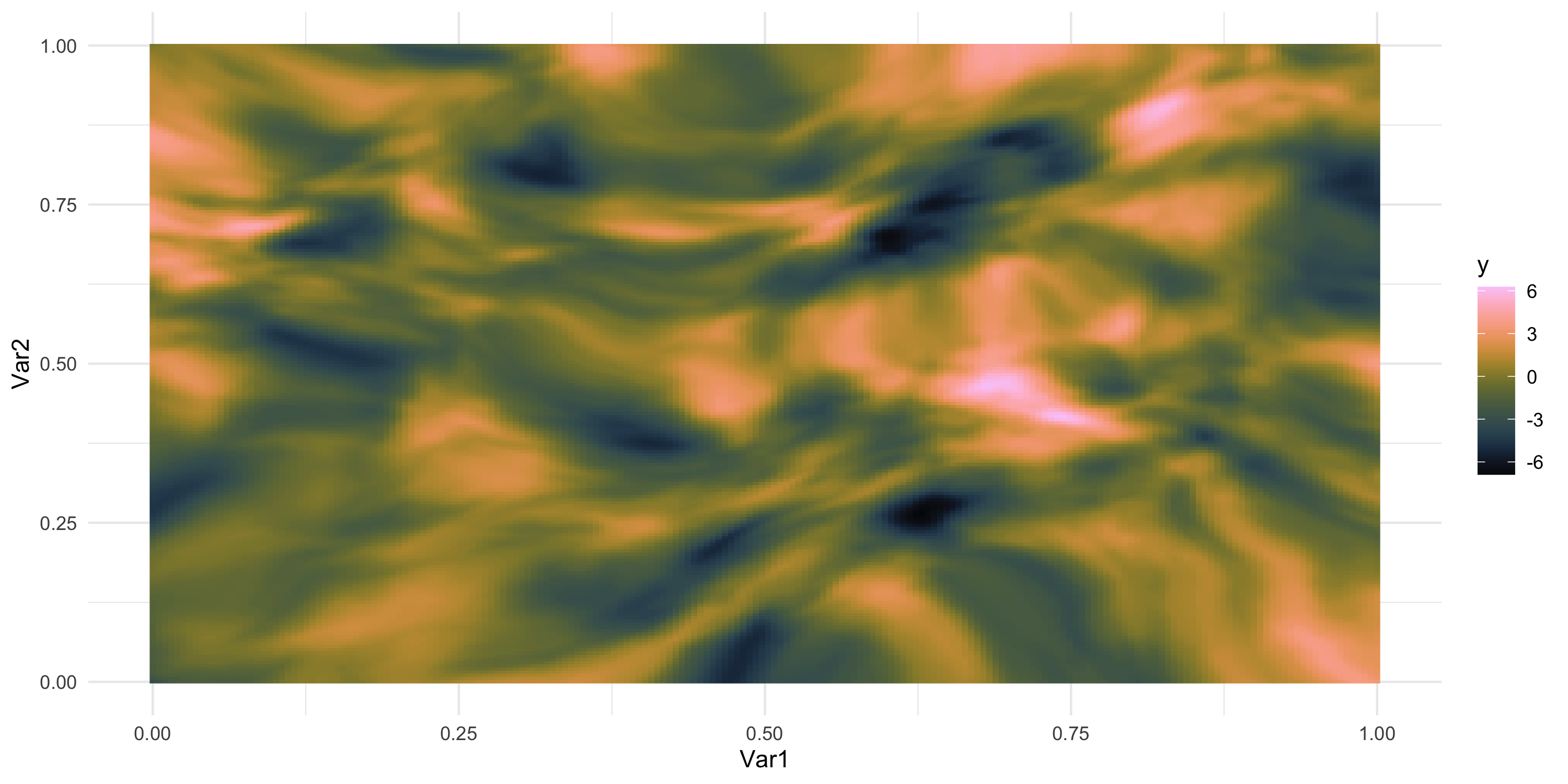
Exploratory analysis and simulation

  • What does spatial dependence “look like”? Example 10

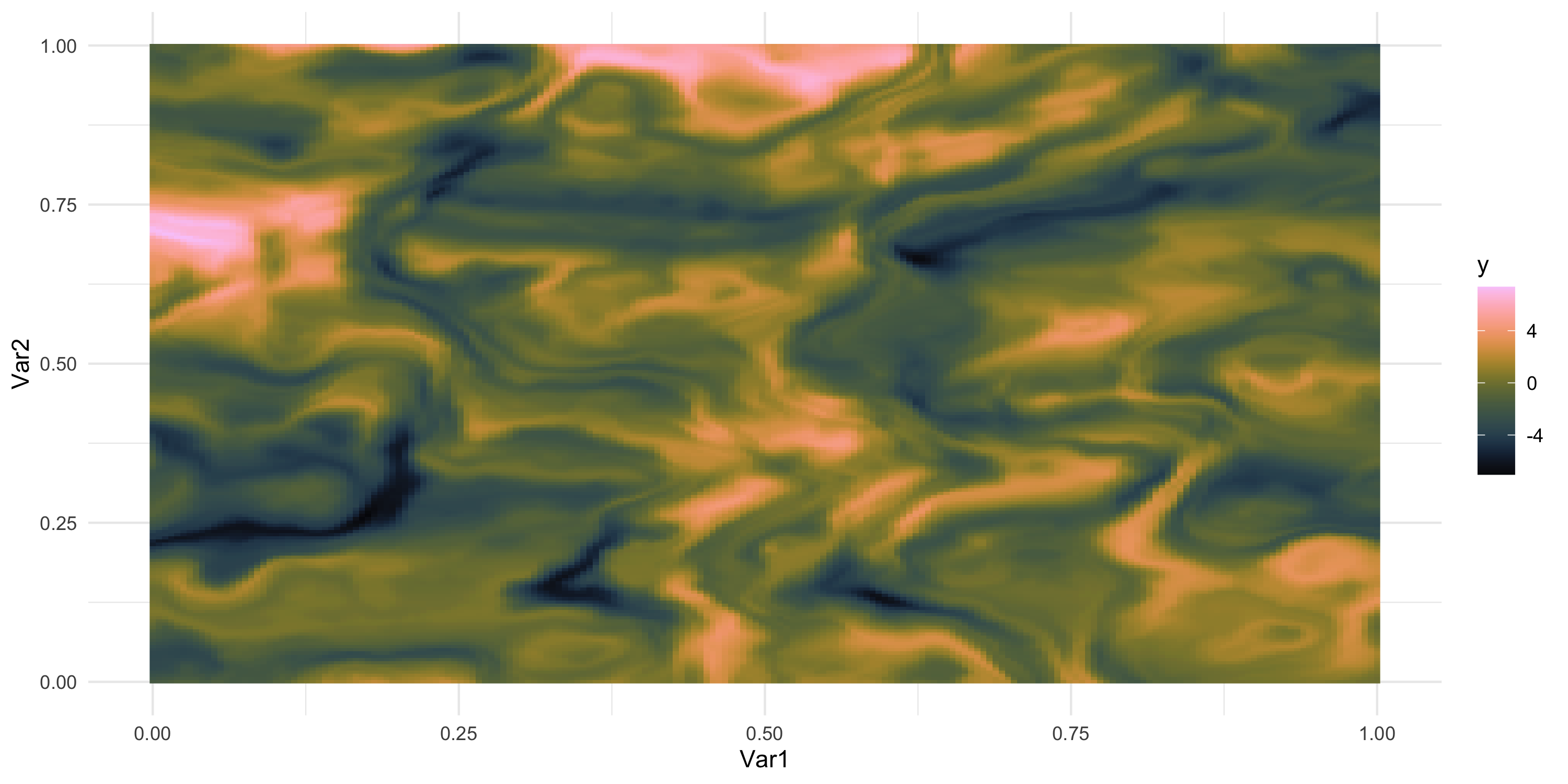
Exploratory analysis and simulation

  • What common feature can we recognize?

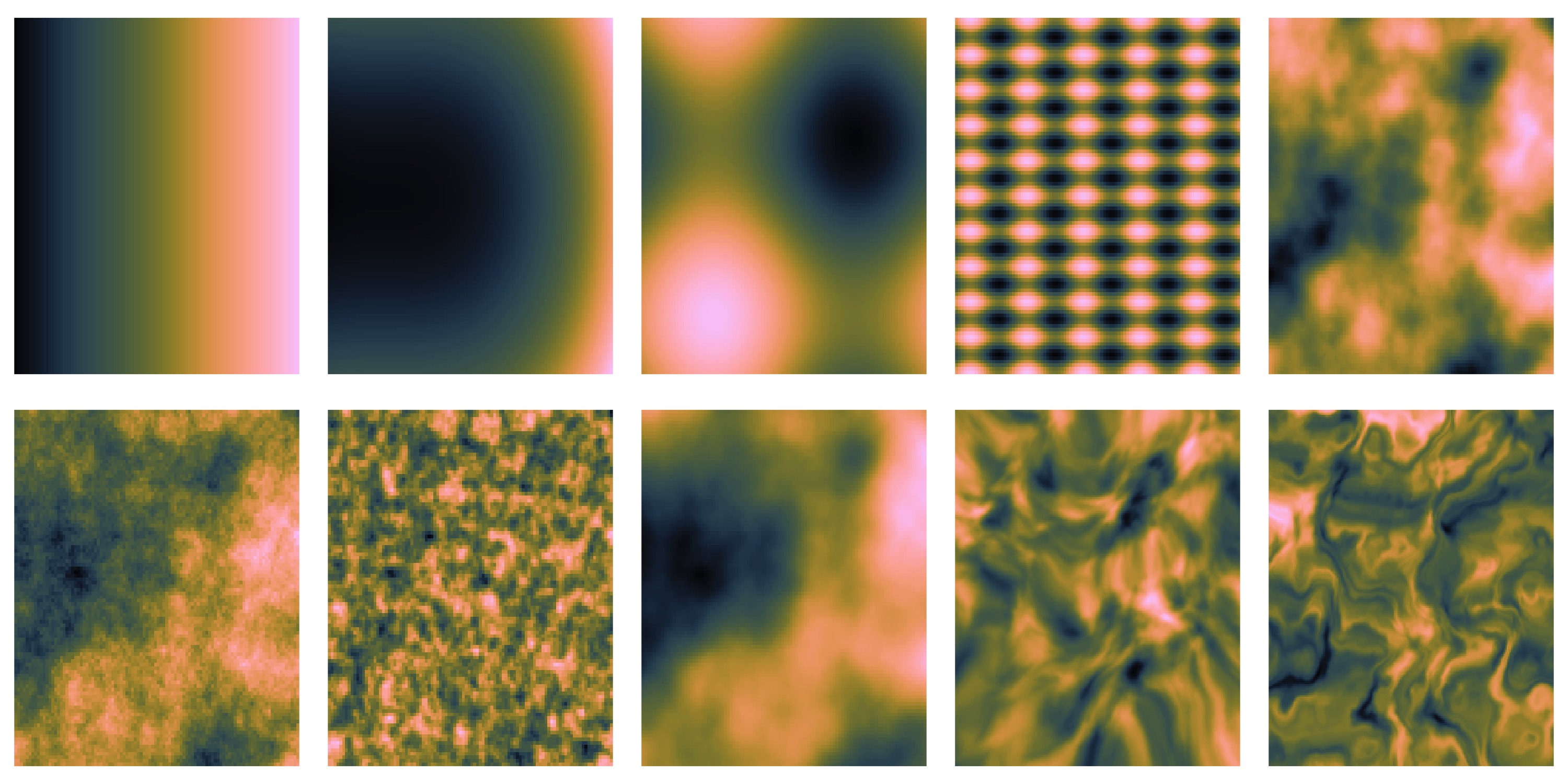
We only observe 1 sample

What if we could “re-run” the data-generation? Different data, same process

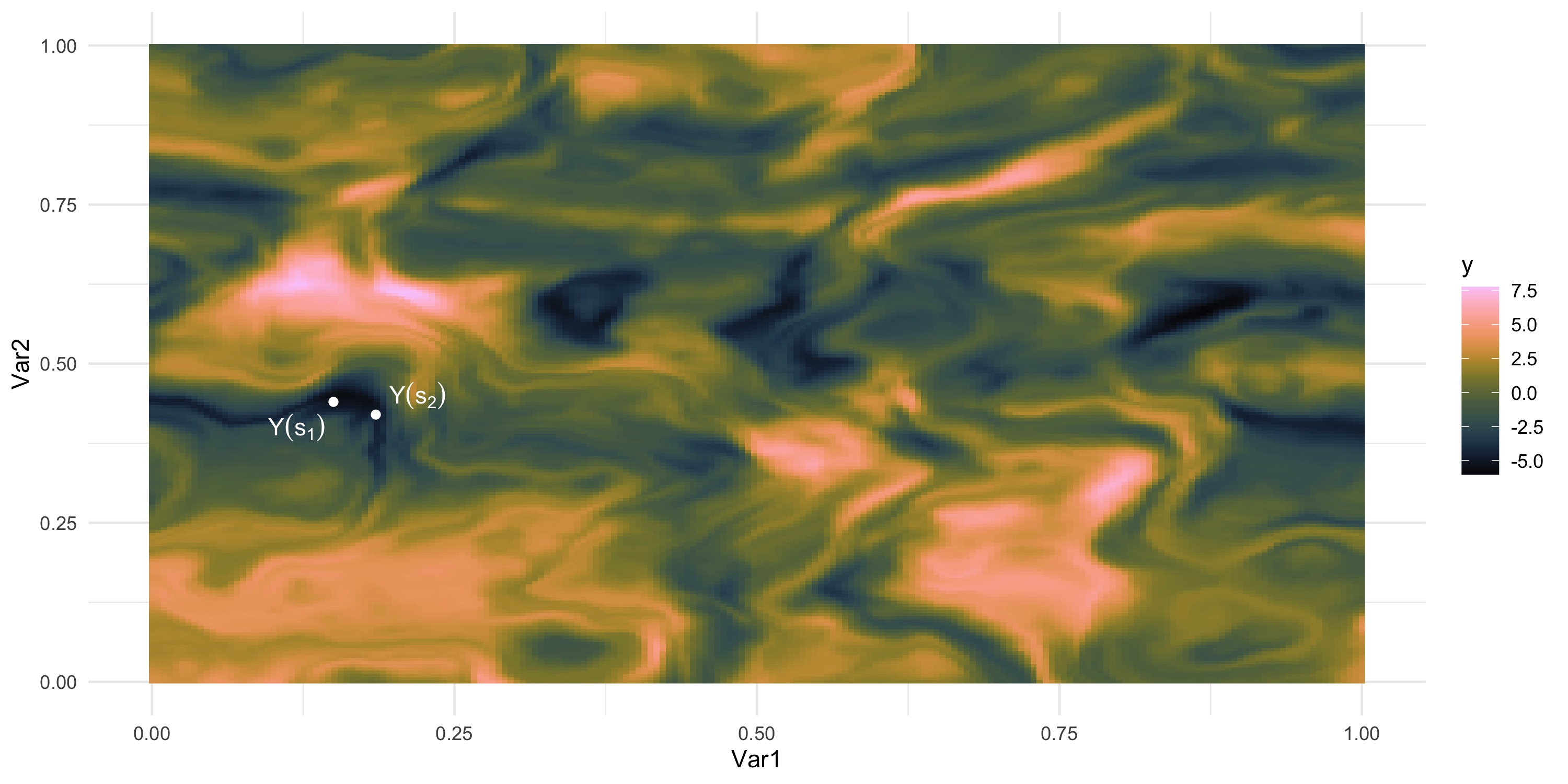
We only observe 1 sample

What if we could “re-run” the data-generation? Different data, same process

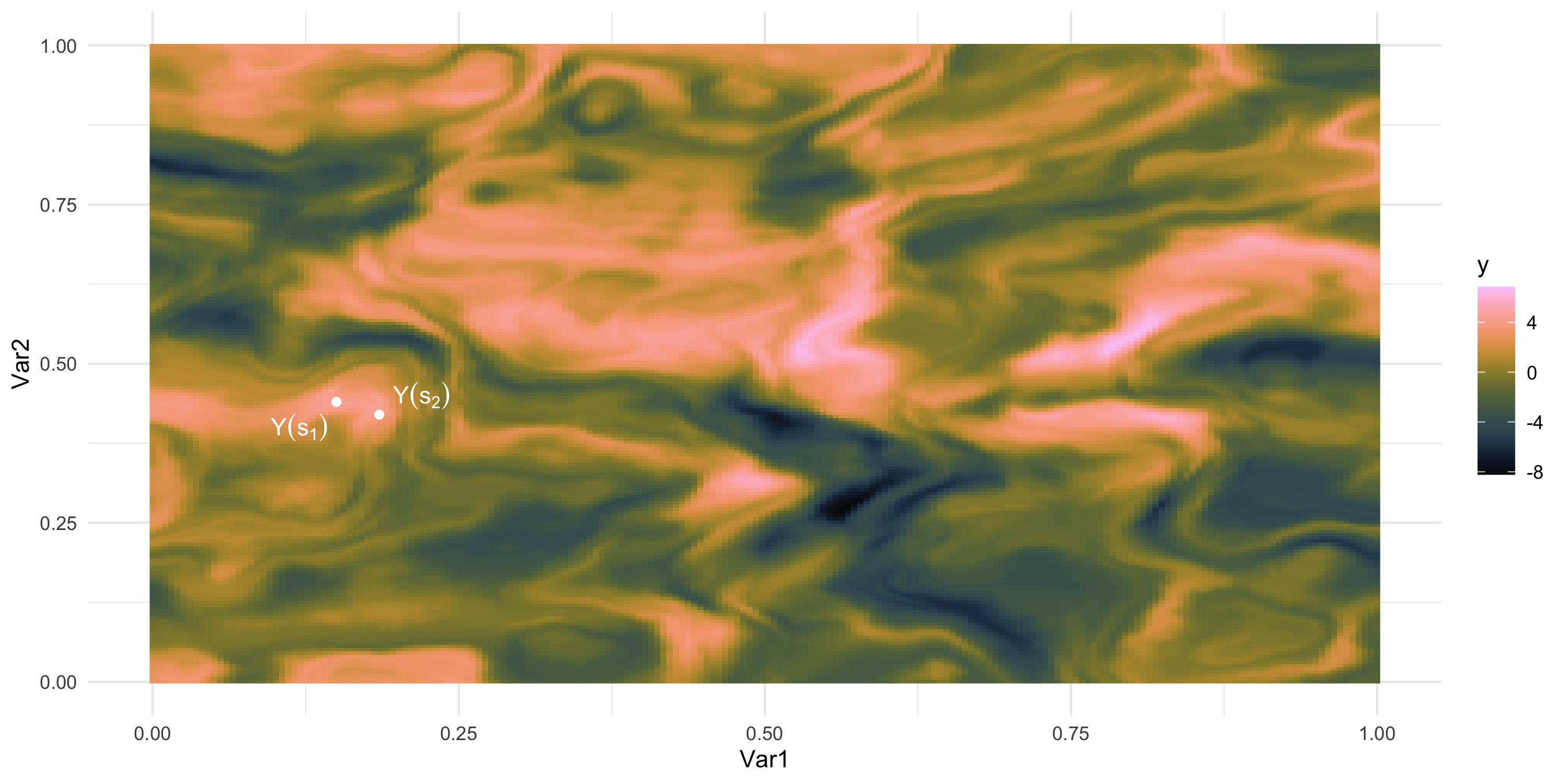
We only observe 1 sample

What if we could “re-run” the data-generation? Different data, same process

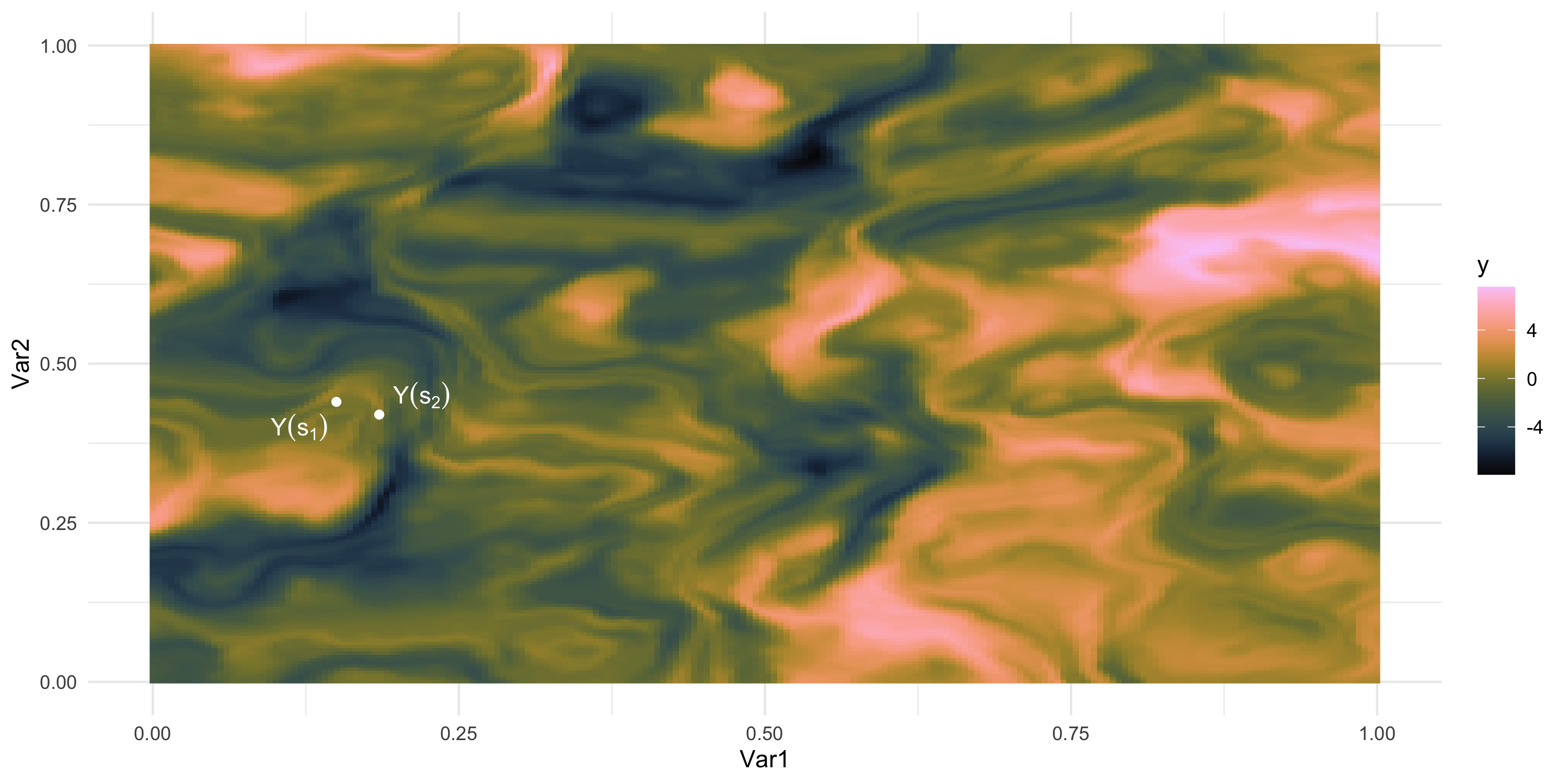
We only observe 1 sample

What if we could “re-run” the data-generation? Different data, same process

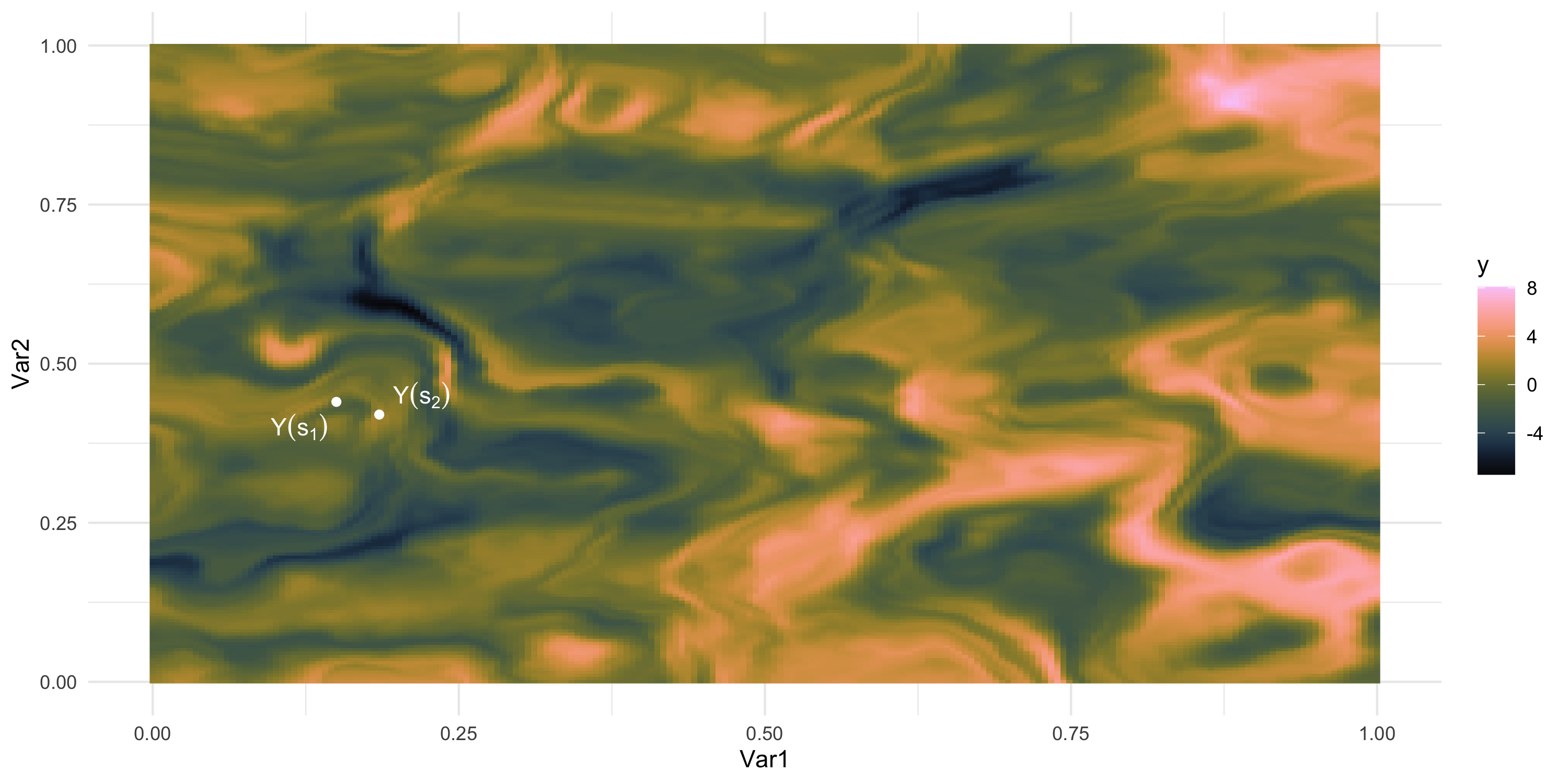
We only observe 1 sample

What if we could “re-run” the data-generation? Different data, same process

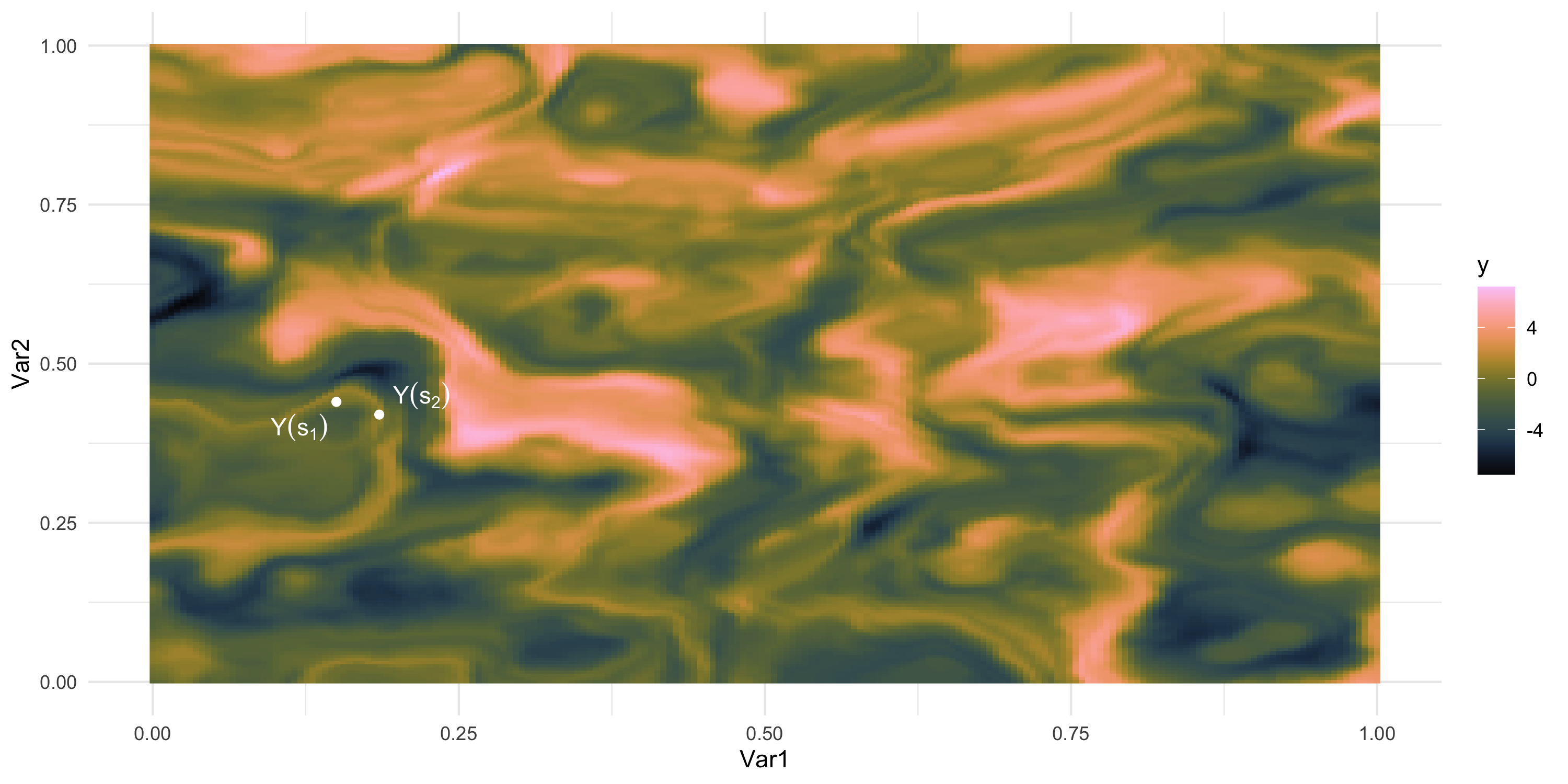
We only observe 1 sample

What if we could “re-run” the data-generation? Different data, same process

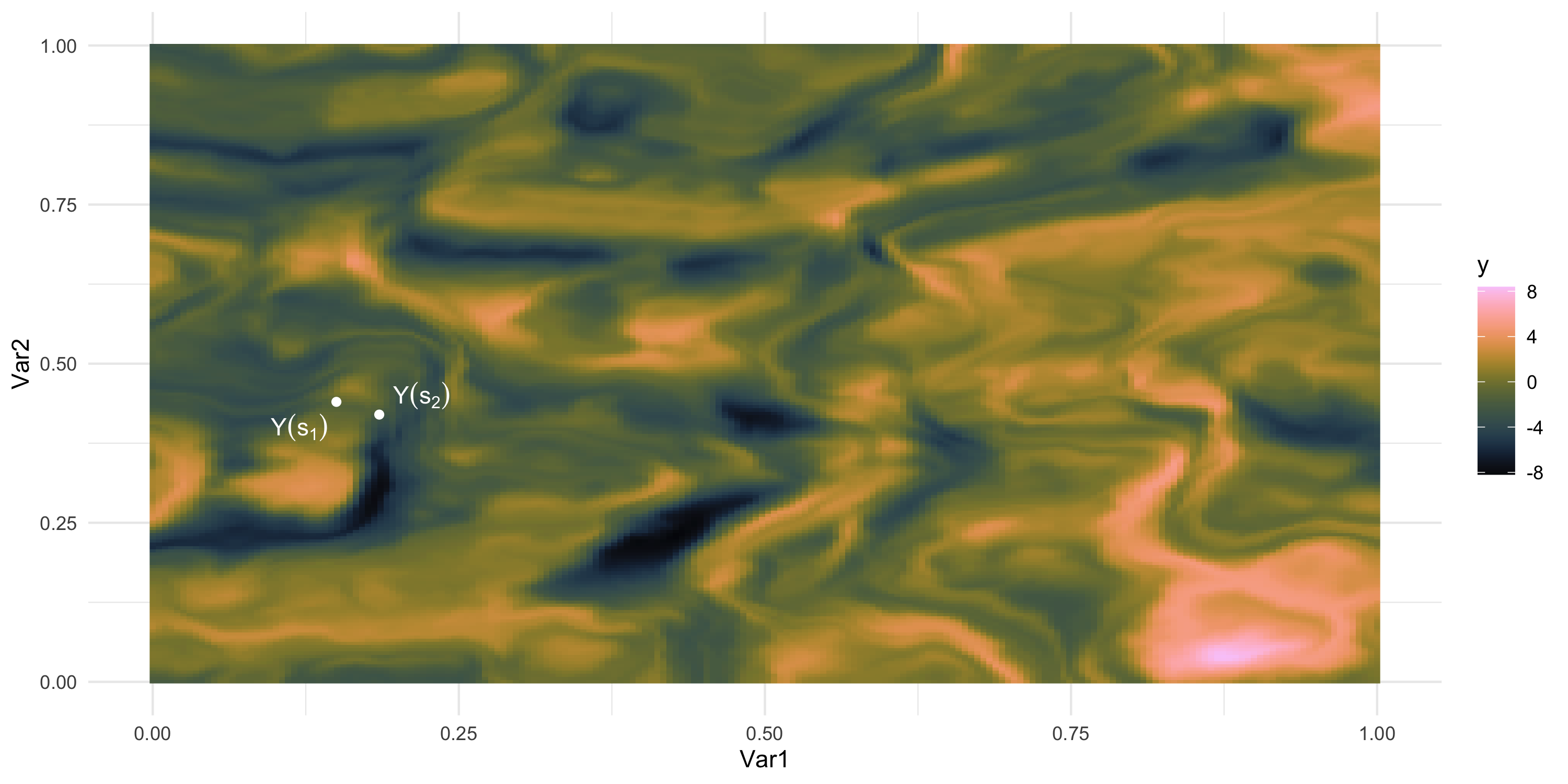
We only observe 1 sample

What if we could “re-run” the data-generation? Different data, same process

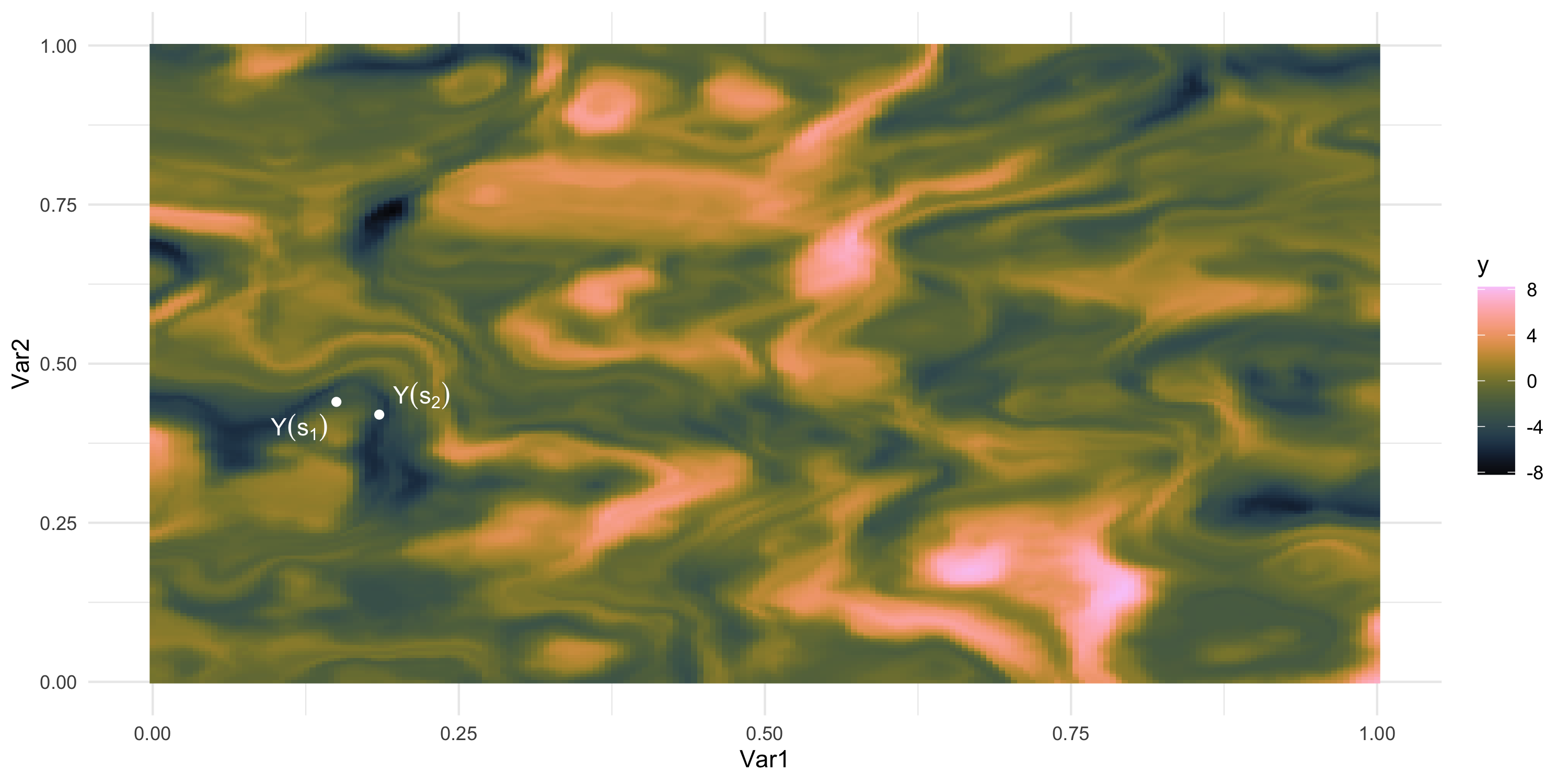
Exploratory analysis and simulation

  • How “similar” are the random variables Y(s_1) and Y(s_2)?
  • In other words, how large do we expect this is: | p(Y(s_2) | Y(s_1)) - p(Y(s_2)) |?
  • Easier? How large do we expect this is: Cov( Y(s_1), Y(s_2) )?

Exploratory analysis and simulation

  • How “similar” are the random variables Y(s_3) and Y(s_4)?
  • In other words, how large do we expect this is: | p(Y(s_4) | Y(s_3)) - p(Y(s_4)) |?
  • Easier? How large do we expect this is: Cov( Y(s_3), Y(s_4) )?

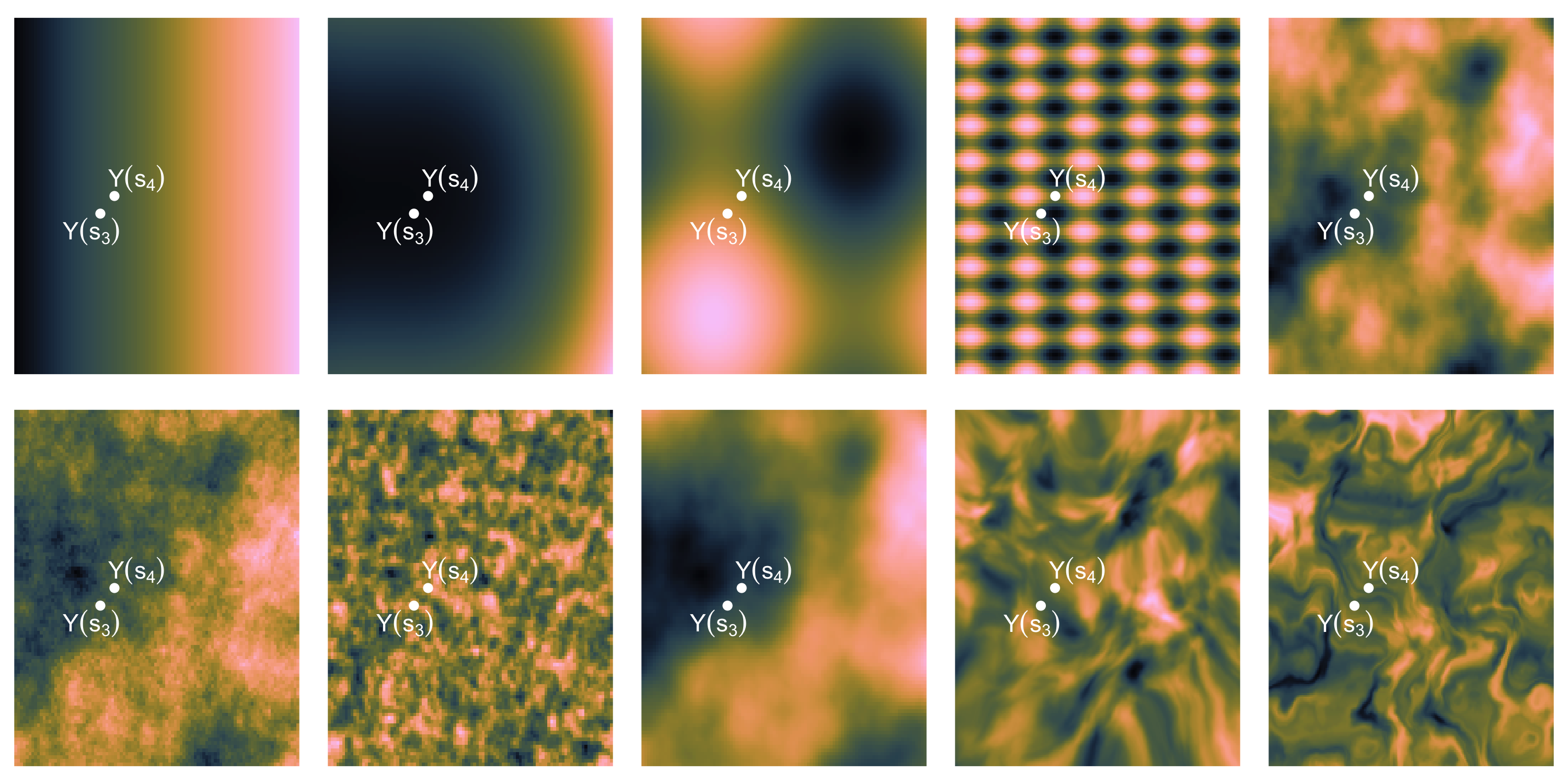
Exploratory analysis and simulation

  • Distance between random variables (largely) drives how related they are
  • If the variables are close to each other in space, then Cov(Y(s), Y(s')) should be larger
  • The question of what model to use for Cov(Y(s), Y(s')) is crucial
  • If we let Cov(Y(s), Y(s')) = g(s, s'), how do we choose g(\cdot)?
  • For example, we could model g(\cdot) as a positive decreasing function of \| s-s' \|
  • We can think of many other alternative models. More on this later…

Exploratory analysis: empirical semivariogram

  • How do we measure spatial association in data before we attempt any sort of modeling?
  • Call Y(s_i) and Y(s_j) the r.v.’s at s_i and s_j
  • Suppose the domain is D = [0,1]^2
  • Partition the line (0, m) \subset \Re into K disjoint intervals
  • I_1 = (0=m_0, m_1], I_2 =(m_2, m_3], \dots, I_K = (m_{K-1}, m_K=m].
  • Define t_k = \frac{m_k - m_{k-1}}{2} (the midpoint of the kth interval)
  • Define N(t_k) = \{ (s_i, s_j) : \| s_i - s_j \| \in I_k \}
  • N(t_k) is a set of all pairs of locations whose pairwise distance is “approximately” t_k

Exploratory analysis: empirical semivariogram

  • Define N(t_k) = \{ (s_i, s_j) : \| s_i - s_j \| \in I_k \}
  • Define the empirical semivariogram as:

\gamma(t_k) = \frac{1}{2 |N(t_k)|} \sum_{(s_i, s_k) \in I_k} (Y(s_i) - Y(s_j))^2

  • What should \gamma(t) look like for increasing t if there is spatial dependence?
  • If spatial dependence, Y(s_i) and Y(s_j) should be close to each other if s_i and s_j are not far apart

Exploratory analysis: empirical semivariogram

  • Define N(t_k) = \{ (s_i, s_j) : \| s_i - s_j \| \in I_k \}
  • Define the empirical semivariogram as:

\gamma(t_k) = \frac{1}{2 |N(t_k)|} \sum_{(s_i, s_k) \in I_k} (Y(s_i) - Y(s_j))^2

  • What should \gamma(t) look like for increasing t if there is spatial dependence?
  • If spatial dependence, Y(s_i) and Y(s_j) should be close to each other if s_i and s_j are not far apart
  • We then expect \gamma(t) to be increasing with t: as the locations are farther from each other, the observations become increasingly different

Exploratory analysis: empirical semivariogram

  • install.packages("geoR") (you may need to install XQuartz in your system)
  • Plot the empirical semivariogram via geoR::variog
  • Let’s use Example 8 from earlier
sv <- simdf %>% with(geoR::variog(data = y, coords = cbind(Var1, Var2), messages=FALSE))

sv_df <- data.frame(dists = sv$u, variogram = sv$v, npairs = sv$n, sd = sv$sd)
sv_plot <- ggplot(sv_df, aes(x=dists, y=variogram)) + geom_point(size=2, shape=8) +
  theme_minimal()

grid.arrange(data_plot, sv_plot, nrow=1)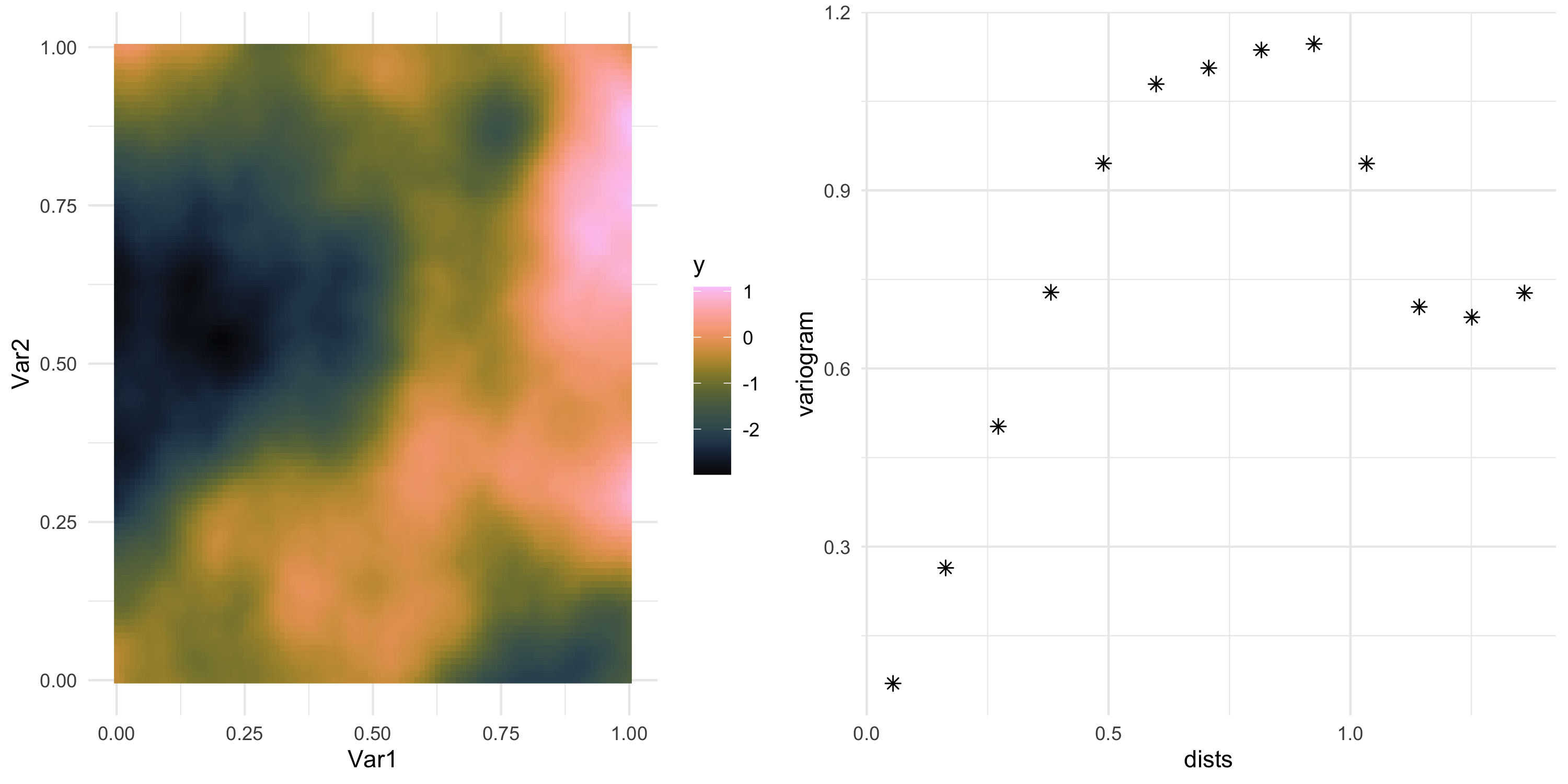

Exploratory analysis: empirical semivariogram

  • Let’s use Example 10 from earlier

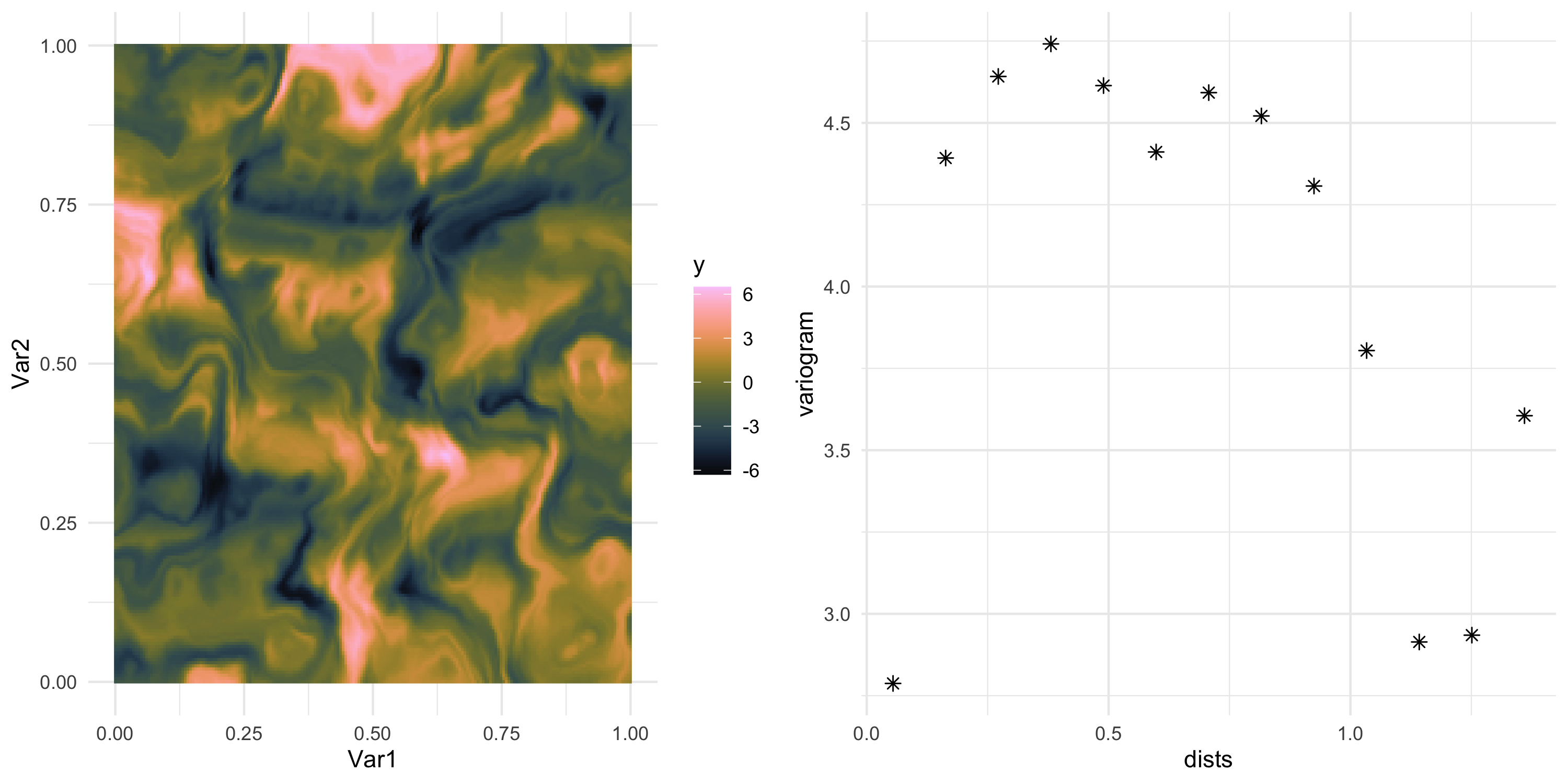
Exploratory analysis: example

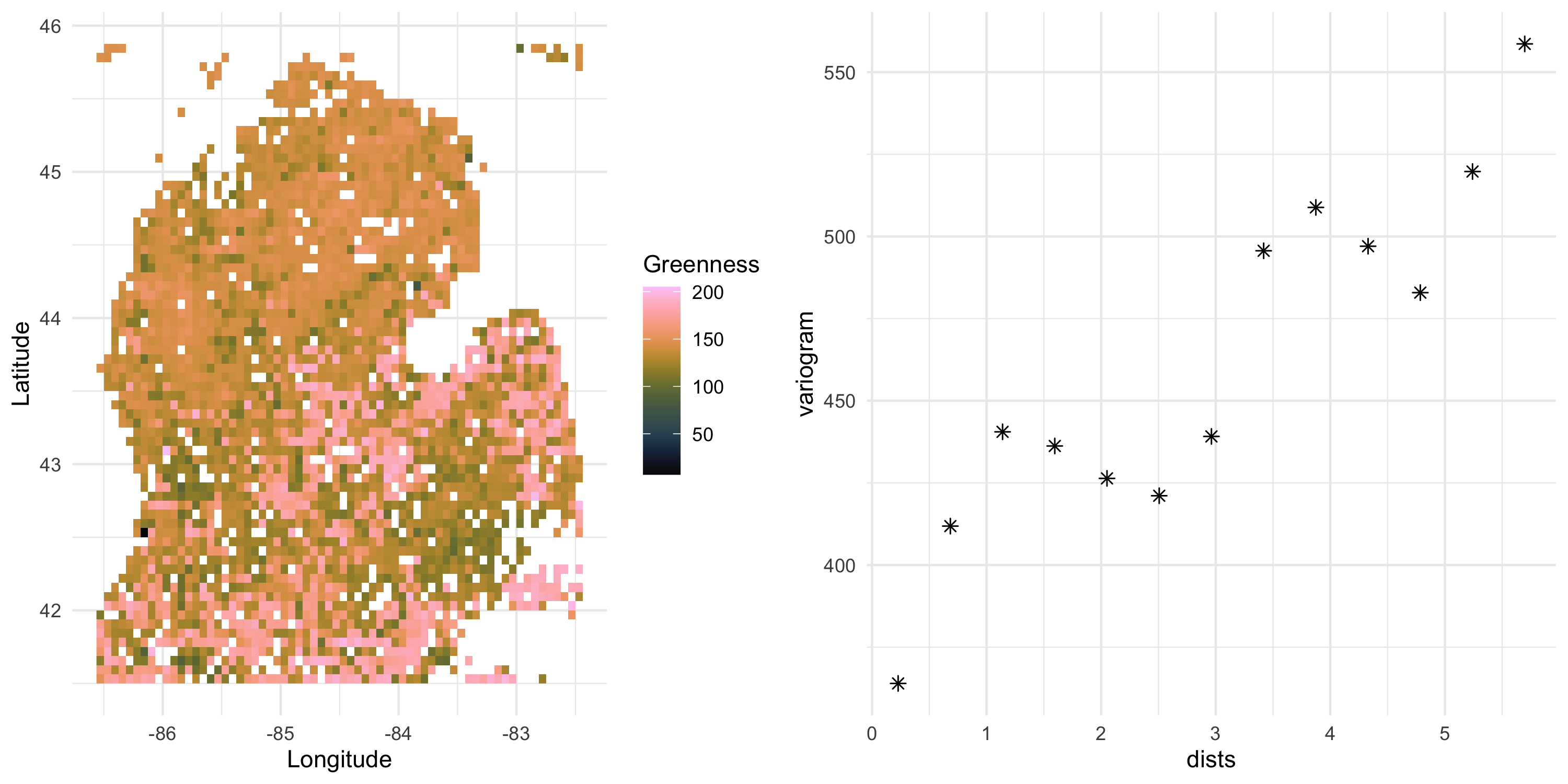
  • We want to investigate a variable representing the time it takes for vegetation to reach peak greenness
  • Changes in the greenup time may be explained by climate change
df <- read.csv("data/michigan_greenness.csv")

(data_plot <- ggplot(df, aes(Longitude, Latitude, fill=Greenness)) +
  geom_raster() +
  scale_fill_scico(palette="batlowK") + 
  theme_minimal())

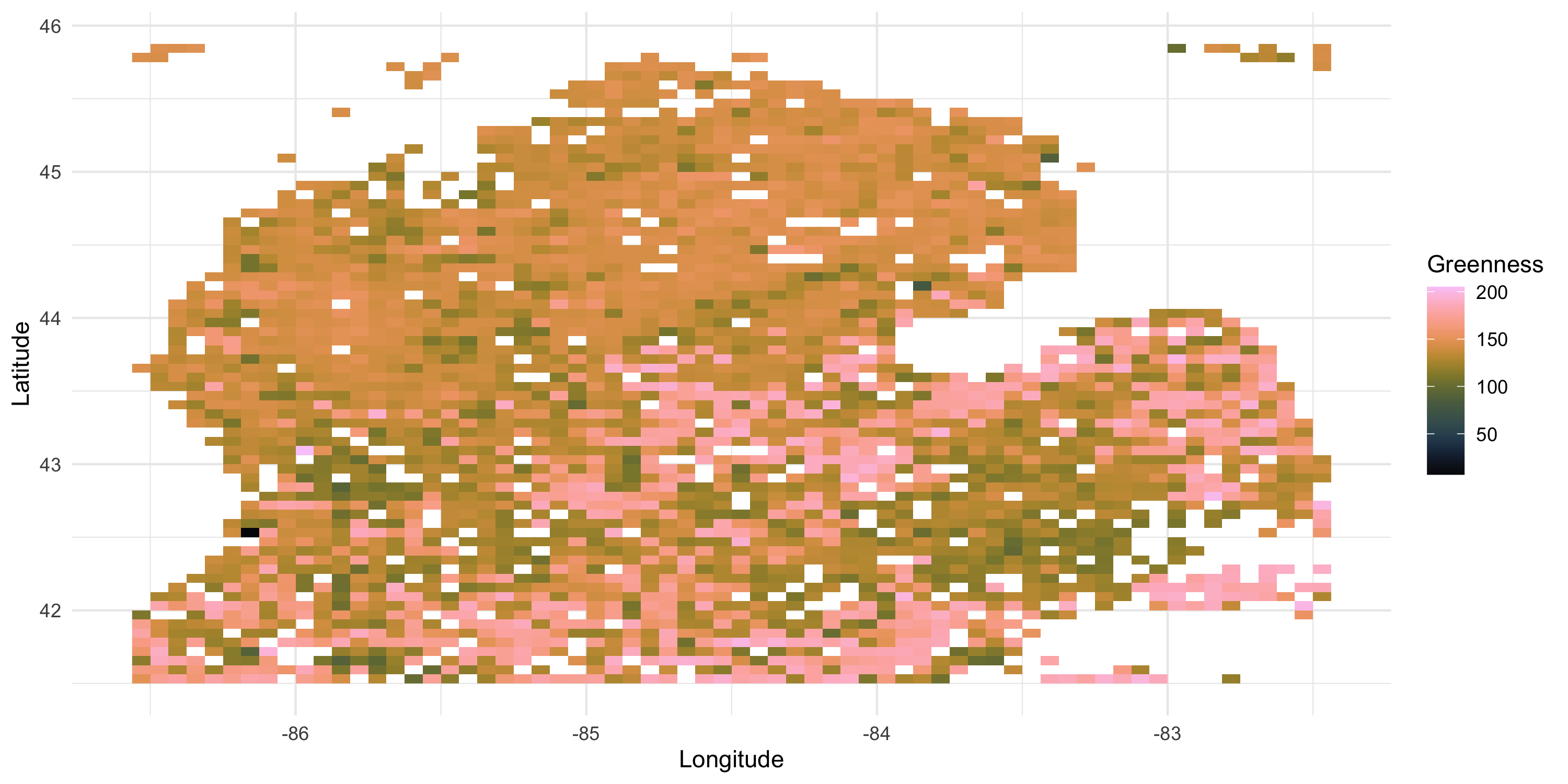
Exploratory analysis: example

sv <- df %>% with(geoR::variog(data = Greenness, coords = cbind(Longitude, Latitude), messages=FALSE))
sv_df <- data.frame(dists = sv$u, variogram = sv$v, npairs = sv$n, sd = sv$sd)
sv_plot <- ggplot(sv_df, aes(x=dists, y=variogram)) + geom_point(size=2, shape=8) +
  theme_minimal()

grid.arrange(data_plot, sv_plot, nrow=1)

Home page